Math Made Easy: Problem of the Day 70: Addendum to Day 69

In yesterday’s article, I conjectured, falsely, that the triangle above does not have a unique solution. The method I used ended with unique measures for all angles excepting four, and three of those four given measures in terms of the fourth. Well, I was wrong. I was, as I have admonished others for doing in the past, focusing so much on the immediate problem of the circular system of equations I produced at the end, that I did not see the forest for the trees. I did not remember my mathematical toolbox and attempt an alternate method to find those last four angles. Today I’ll use an alternate method to find them, and we’ll see that it works. The triangle absolutely does have a unique solution.

First, let’s remind ourselves of what our angle measures were when we left off yesterday.

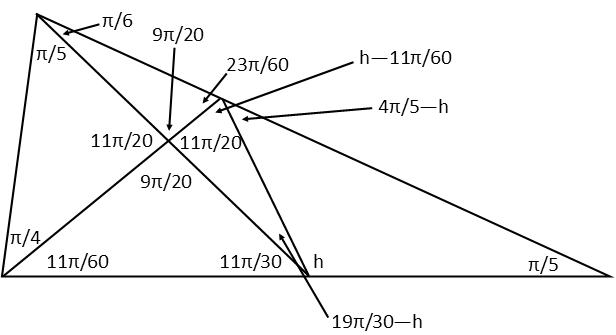
Now, we’re going to make an assumption. Let us assume that the bottom leg of the big triangle has a length of 1. I am giving it an arbitrary measure to achieve what I’m about to do, so it can be anything I like. 1 is as good a number as any, so I’ll start there. I’ll now also label all the sides of the triangle with a variable.

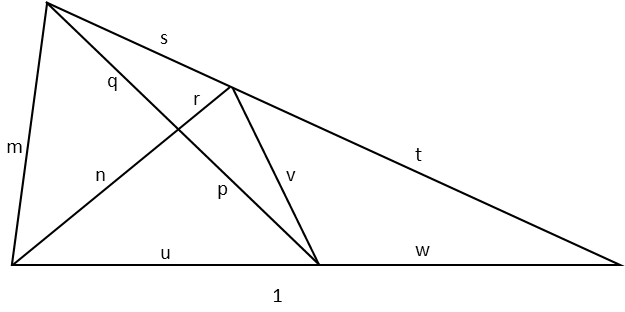
That done, we can find all the sides using a combination of the Law of Sines and the Law of Cosines. The Law of Sines will work for every side but one. Remember that, for the Law of Sines, you’re simply stating that the ratio of one side over the sine of its opposite angle is equal to that same ratio for any other side in the same triangle. So to use it, I must know the measure of two angles and one of their opposing sides, or two sides and at least one opposing angle. It is not useable when you have only an included side and the two adjacent angles, or an included angle and its two adjacent sides – that’s when you need the law of cosines. So below see the math for all the sides in the triangle that can be found using the Law of Sines. Note I follow an order dictated by the sides known as I find them. For finding angle t, I used the side r+n and its opposing angle in the triangle formed with those two sides.

When we get to that last side, v, we see that, for both the triangles of which it is a part, we end up with two variables when we set up the Law of Sines – we know v’s opposing angle, but not v, so there’s a variable in that ration, but on the other side of the equation, we don’t know the either candidate angle, which means we have a second variable. So we cannot use the Law of Sines here, either. But we do know enough to use the Law of Cosines, since we know v’s opposing angle, and we know the other sides. Exactly what is needed for that particular law. So we now remind ourselves of the form of the Law of Cosines and plug in the known sides and angle to find our final side.

And here’s what our diagram looks like with the measures of the sides filled in. Note that I found w by simply subtracting side u’s measure from 1.

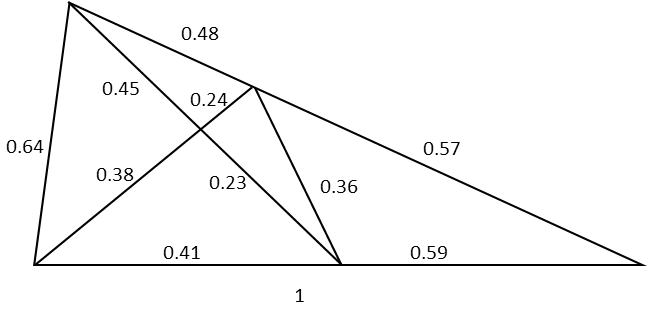
Now we are ready to find the measure of the remaining angles. Since I already related three of them in terms of angle h yesterday, I will use the Law of Sines to find it, then I will simply plug that value into the expressions I found for the other three angles. Note here that, since we’re using the Law of Sines rather than simple angle addition, we won’t get a nice fraction for angle h. Also remember that, to undo a sine, or find the angle inside the sine function, you take the inverse sine function to do so.

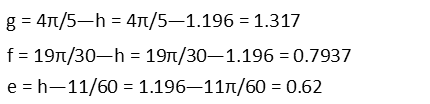
Here’s what the completed triangle with all angle measures looks like, again, not corrected for scale:

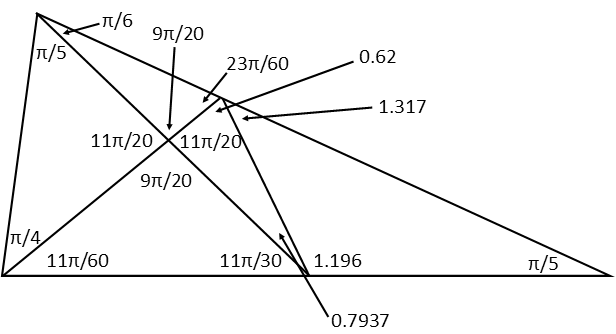
Even the best of us can fall for the trap of being blinded by an immediate problem within the greater problem we’re working, and fail to remember that we have other tools we can use. Try your best not to fall into that trap, lest you deem a problem to have no solution when it does, indeed, have one.