Math Made Easy: Problem of the Day 71

While this may appear to be a puzzle in three dimensions, it really isn’t. Since the wire is wrapped around the outside surface of the cylinder, its dimensions relative to the cylinder can be represented in a two-dimensional Euclidean space. To do this, let’s imagine cutting the cylinder down its length and unrolling it. If you have difficulty envisioning this, go grab a toilet paper roll, draw a line wrapping around its outside surface from top to bottom, then cut the roll down its length.

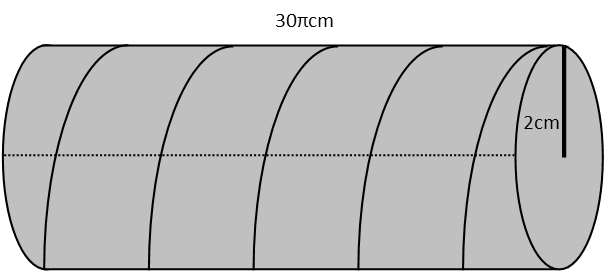
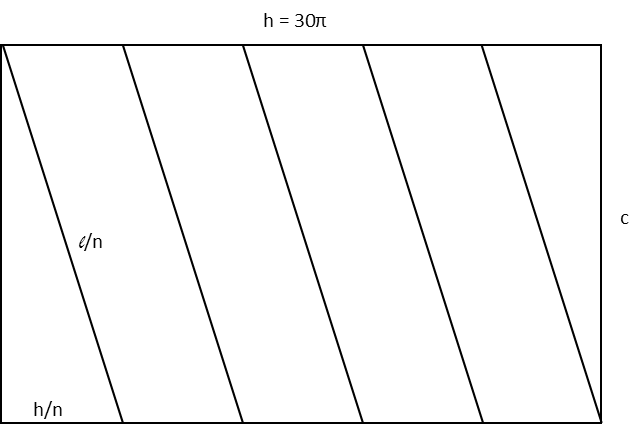
What we see when we cut the cylinder and roll it flat, is that the wire isn’t actually making arcs as it appears to be doing when the cylinder is still rolled up. The wire actually makes straight lines, each of which is forming the hypotenuse of a right triangle. The sum of the length of those hypotenuses will equal the length of the wire. We can also see readily that there are a number of hypotenuses equal to the number of wraps around the cylinder the wire makes. So each hypotenuse length is equal to the length of the wire dividing by the number of wraps. The same can be said for the bases that follow the length of the cylinder, only their lengths are determined by the height of the cylinder divided by the number of wraps. We also see that the height of each triangle is equal to the circumference of the cylinder, since that now is a straight line. I’ve labelled those accordingly in my diagram of the flattened cylinder.

Now let’s look at one triangle. We can draw a diagram of it with our proper labelling.

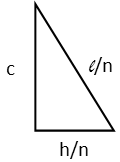
To find n, we can use the Pythagorean Theorem. We remind ourselves of it, plug in our expressions for the hypotenuse (c), and the legs (a and b, it doesn’t matter which we call which). We then distribute the squares, and move everything with an n in the denominator to the same side of the equation. (Note the c in the first equation, before things are plugged in, is not the circumference of the circle, but just labelled by convention. The c in the equation once everything is plugged in is the circumference)

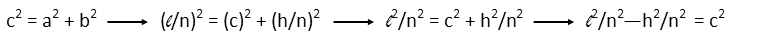
We made that move so we can combine those two fractions into one. Once we do so, we remember we’re trying to solve for n. We don’t want it on the bottom of the equation, so, since we now have it in a single fraction, we take the reciprocal of both sides of the equation. Bam, n is now on top. This allows us to move all the junk under it back to the other side of the equation by multiplying both sides by the junk (I like calling a group of terms junk just to remind myself I can treat it as such while I’m just moving it around). Once we’ve done that, all we have left is to take the square root of both sides.

Now that we have a satisfactory equation that solves for n, we can look to plugging in our values. First, though, we need to calculate the circumference of the cylinder. Since it’s radius is just 2cm, that’s pretty simple, we find it so:

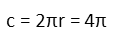
When we plug in all our values, and square, we see we have a convenient happenstance where the π’s all cancel. This gives us an integer number of terms - our wire wraps around the cylinder exactly 10 times.

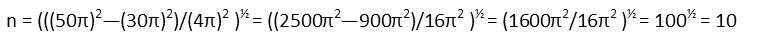
Now, this problem could have been solved a couple other ways. One method would be to use parametric equations and integrals. However, that method is actually MORE complicated than simply breaking it down and using Euclidean Geometry to solve the problem. And since Calculus was invented to make very complicated problems easier, we really shouldn’t use it to make relatively simple problems more complicated. That completely defeats the purpose of having a mathematical toolbox at your disposal.

For an added challenge, find the maximum number of times any wire could wrap around this cylinder, and the wire's length.