Math Made Easy: Problem of the Day 72

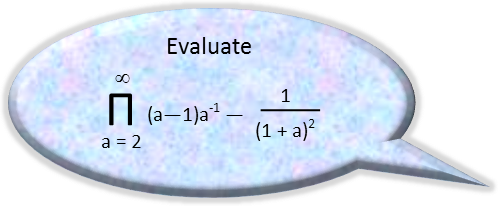
Happy Pi Day! And since Pi is an irrational number that goes on forever, what better way to celebrate Pi day than evaluate an irrational product that goes on forever? The notation in the problem above may not look familiar to many people, but it is called Pi notation, and it is similar to a more common form of notation called Sigma notation. While the latter is a short way to write complicated and lengthy sums, the former, Pi Notation, is similarly a short way to express complicated and lengthy products. So when you see Pi notation, it is saying “Plug this bottom number in for the equivalent variable everywhere you see it in the expression, then multiply that by the next number up plugged in, then by the next, and so on until you reach the number on top of capital Pi.” So, we do something like this when we see it:

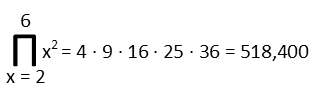
Now since we have an upper end to the domain of our product of infinity, we might be tempted to evaluate it as infinity. But we see two fractions in our expression, both of them with the variable in the denominator. That means our product might not be divergent to infinity. It might actually converge on something, possibly between one and zero. Let’s look at the graph of the function to get an idea of what’s going on.

Well, that’s interesting, but that graph isn’t quite helpful for what’s going on in the domain we’ve been given, so let’s shift it and zoom in a bit.

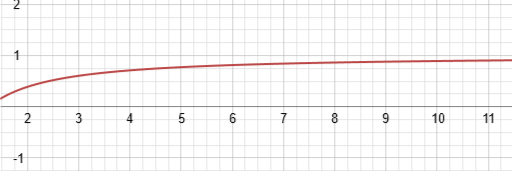
Okay, that’s better. It looks like it’s converging on 1 as it approaches infinity. Let’s manipulate the function a little bit to see if we can get it in a form that confirms this appearance.

First, we’re going to give those two fractions a common denominator. (Don’t see the two fractions? Remember that -1 exponent just means the term with it is on the bottom of a fraction). Doing so and combining the fractions, we get:

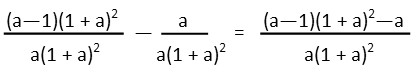
Now let’s factor the squared binomial in the numerator. This is actually useful, because it lets us see the difference of squares up there. That allows us to multiply that out first, giving us two binomials.

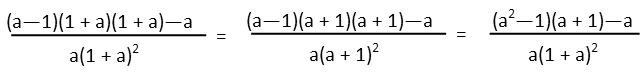
Multiplying those binomials in the numerator, we get a cubic. Consolidating the terms in the cubic whilst evaluating the square in the numerator and distributing the a into the result, we get:

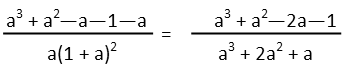
Now we have a result that confirms our graph. Since the degrees of the polynomials in the numerator and denominator are the same, we recognize that a horizontal asymptote exists where y is the ratio of their leading coefficients. Both cube terms have a coefficient of 1, so that means the horizontal asymptote exists at y=1. That means the function converges on, but never reaches, 1. This also tells us that as a gets bigger, the fraction is closer to one, so each term succeeding term being multiplied effects the product less and less. BUT, each succeeding term is still a fraction. Any time we multiply a fraction by a fraction, we get a number smaller than either fraction. So our product gets smaller and smaller and smaller the more terms we multiply.

This means our product converges on, but never reaches, zero. It does so more slowly the more terms we add, but it does so nonetheless. We needn’t bother multiplying out the terms (but you can if you like, just to prove it to yourself). So our result is infinitely small, infinitely close to zero, but not quite. It is an infinity within an infinity within an infinity. I love things like this, and love showing them to math students when they’re just beginning to explore concepts of numbers beyond the every day. It’s fun to contemplate the fact that, as big as infinity is, you can, and do, hold it in the palm of your hand.