Math Made Easy: Problem of the Day 73

Ambiguities have existed in mathematics since man started adding numbers on his fingers. Far less exists today than even a century ago, but this is entirely due to mathematical societies around the world coming together and agreeing to conventions that eliminate ambiguity. After all, if anyone sees a math problem, no matter who they are, they should be able to work through it and achieve the same answer that somebody else on completely the opposite side of the world in a different culture achieves. And yet, many ambiguities still exist.

These ambiguities arise from the fact that math really ISN’T a universal language. Math is the tool. But the notation we use to express our math – that is the language, and it's not universal. Languages evolve, and languages introduce confusion. Especially when those languages were created separately in different locales. Historically, mathematicians used to have to list at the beginning of their work all the conventions they were using in their notation, as well as descriptions of what some of the meanings of their notation. We’ve done away with the need for most of that, BUT, because of the differing cultures in the world, and because different mathematicians developed different symbols and methods for doing the same things, there do still exist places where confusion exists.

Take the symbol for division, for instance. We have at least 5 of them: the obulus ÷, the slash /, the colon :, the vinculum – (or fraction bar), and a closed parenthesis ), though the last one you usually only see used in conjunction with the vinculum for use in long division. This introduces all KINDS of confusion, especially when people from different cultures are attempting to communicate their mathematics. Just what does that symbol mean? Is it division? If a vinculum is used in between two numbers horizontally instead of vertically (as in 6 – 5), do they mean division or subtraction? Thankfully most of the world is agreed on subtraction for that last one.

So today’s problem is all about ambiguity in notation. There are three different, and all correct, approaches to the problem. I’ll address all three in turn, and try discuss advantages and disadvantages to each.

First, let’s use good ol’ PEMDAS (or BEDMAS, BIDMAS, or BODMAS as it is in some other cultures – again, confusion!). If we attack this by strict order of operations from PEMDAS, we work everything inside the parentheses first. But here’s where some more ambiguity comes in. If we go STRICTLY by the acronym, in America all multiplication comes before division. But in the other cultures (Canada and Britain use the B ones), all division comes first. And yet many in all three cultures will argue that multiplication and division have equal precedence. The last argument is the most prevalent, so I’ll handle PEMDAS that way – by giving multiplication and division equal precedence, and work left to right, but everything inside the parentheses first. I’ll also rewrite the problem removing the implicit multiplication in favor of explicit multiplication symbols and replacing the slash with an obulus. Doing it this way, I’ll stay in steps to demonstrate.

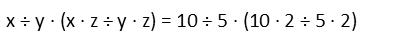
Our result going by strict PEMDAS, with multiplication and division being given equal precedence left to right, we get 16. Most standardized tests go with the strict interpretation here.

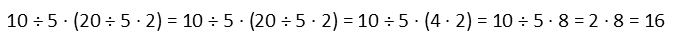
Now for the method I actually think is better. This method accounts for implicit multiplication, and gives it a precedence higher than explicit multiplication. The difference between implicit and explicit multiplication, is the latter exists when a multiplication symbol is used, while implicit exists whenever two things are grouped together with no intervening operators, like 2x, xy, 4(x+y), or the like. In our problem, we have three cases of implicit multiplication. Two inside the parentheses, and then the y on the outside of them. I’ll rewrite the inside of the parentheses as a fraction, and introduce more parentheses to group the implicitly multiplied terms together to eliminate ambiguity.

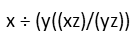
When I do this, we quickly see that the zs inside the parenthes cancel, and the y outside the parentheses cancels the y inside. We’re left with just x ÷ x = 1.

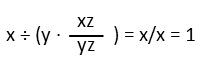
I argue in favor of this method for a few reasons. First, making use of implicit multiplication allows for less writing in our notation. This is a good thing, as the whole point of mathematical notation is so that we don’t have to write all our math using words and sentences, as mathematicians had to do centuries ago. When working on lengthy problems, we want to reduce the amount we’re writing. But to make use of implicit multiplication, we must be able to avoid ambiguity. And since, when we use it, terms are clearly grouped together, it’s best if those terms STAY grouped together instead of us having to break them apart to make use of order of operations, and a strict use of the order of operations requires. Keeping them grouped together makes sense, and is much more elegant, as we just saw. It also allows for much more rapid solutions. FURTHER, giving implicit multiplication precedence, and keeping implicitly multiplied terms grouped, follows with the definition of an operator: a device used to tell the reader to perform on the object to the left some manipulation with the objects on the right of the operator. To be clear: “Take this stuff to the right of me, and use them to change this thing to the left of me in this manner. So 5 + 6 is saying: “change 5 by making it 6 bigger.” Since there is no operator in implicitly multiplied terms, it makes sense to keep them together, and treat them as the object on the right that is being used to change the object on the left.

There is one last way to do this, and it is sort of a combination of strict interpretation of order of operations and giving higher precedence to implicit multiplication. But here, the key is the difference in the division operators. The slash tends to be used more often when we’re dealing with fractions. In that instance, the grouping inside the parentheses makes us think that the two terms to the left of the slash belong on top of the fraction (in its numerator), and the two terms to the right belong on the bottom of the fraction (in its denominator). In this manner, we can treat the terms outside the parentheses as one fraction being multiplied by the fraction that is the terms inside the parentheses. Now we see only the zs cancel, yielding a result of x²/y², or 4 when evaluated for our problem.

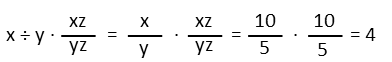
I like this method perhaps least of all, because it is the most ambiguous – it relies on the different division operators being treated slightly differently, as well as treating implicit multiplication grouping differently depending on where the parentheses are.

So don’t be afraid if you’ve seen meme’s online using similar ambiguities in notation, and you got a different result from everyone else. Those meme’s are meant to make people feel clever, and they’re exploiting the ambiguities that exist in notation. Personally, I think those confusions need to be addressed once and for all.