Math Made Easy: Problem of the Day 74

Hopefully by now you’re getting the hang of cross-sectional geometry problems like this one. Always remember to diagram your situation, see what shapes you can find in your diagram that you can solve, and decide if you need to add or subtract them to get your solution.

So let’s diagram what’s going on first. We recognize that the wall makes one side of the yard, and that the leash forms the radius of a semicircle which the dog can describe if it goes to the length of its lead, were the yard big enough to allow it to do that.

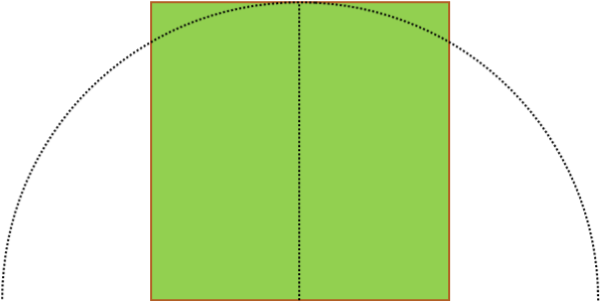
Seeing this diagram, we can recognize that, if we draw a line from the base of the lead to the edge of the arc of the semi-circle that ends where the yard ends, we from a right triangle. Doing this also forms a sector. The right triangle has a hypotenuse equal to the radius of the semi-circle (or the length of the lead), and a base equal to half the length of the wall. If we can figure out the area of the right triangle, and the area of the sector, we can find the total area of the yard accessible to the dog by doubling both and adding them (since we can see in our diagram we have two triangles and two segment).

Finding the area of the right triangle is easy, since we have its hypotenuse and base. We can use the Pythagorean Theorem to find its height:

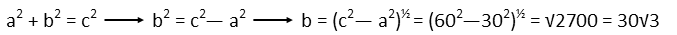
From that, we remind ourselves that the formula for the area of a right triangle is just a special case of the general formula for the area of a triangle, plug in our base and height, and solve:

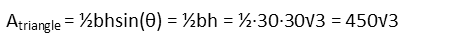
To find the area of the sector, we need to know the measure of the arc. The arc’s measure is equal to the measure of the angle that describes it. And we can see that the angle that does so, angle A, is complimentary to one of the angles of our right triangle, angle B. And since we know the sides of the right triangle, we can just use an inverse trigonometric function to find angle B. I’ll use the cosine since it involves the adjacent side and hypotenuse, so I won’t have worry about that radical in the length of the opposing side.

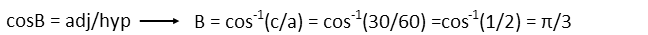
Knowing the unit circle, I know that an angle with a measure of π/3 radians also has a measure of 60 degrees. This means the complimentary angle to it is 30 degrees, or π/6 radians. There are 2π radians in a circle. So the sector is 1/12th of the circle. So we find its area by multiplying the area of a circle times that fraction.

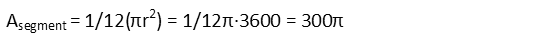
Now that we have the areas of the right triangle and the sector, finding the total area accessible to the dog is a cake walk.

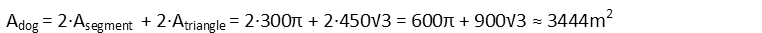
And we’re done! Diagram your situation, break it down, and do the math as you can see each piece, and many problems practically solve themselves. This one really wasn’t all that hard once broken down, now was it?