Math Made Easy: Problem of the Day 75

One might think one needs calculus to solve today’s problem since it involves finding a minimum. But, in fact, if we use our reason to think the problem through, we find we do not. A bit of thought, some knowledge of geometry, trigonometry, and basic algebra is all we need.

First, let us consider what situation would produce the shortest possible cable. In that situation, the cable would be stretched taught with no slack. This would produce a slight arcing around part of the circle, and two straight lines in the cable. Those lines would be tangent to the circle. So, following from the speaker to the cable would be a line tangent, then, when the cable hits that point, it curves around the platform, following the circumference, until it hits the point on the platform on the other side where it can again from a tangent line directly aiming to the outlet. Anything else would produce slack which would add to the length of the cable.

Given these conditions, let’s first draw a diagram of our situation with the taught cable. I will label it with all our distances, and I will also give it a Cartesian coordinate system, with the origin at the center of the circle – I can do that because I can place the origin wherever I like. This will prove very convenient to our math. I’ll go ahead and label the coordinates of the a few known points based on our system, too. Since our outlet is six meters from the speaker, and the platform directly in the center, we can reason that the outlet and speaker are both 2 meters away from our 1 meter radius platform (since it takes up two meters of that space – its diameter). Assigning coordinate values equivalent to our distances also helps make the math convenient.

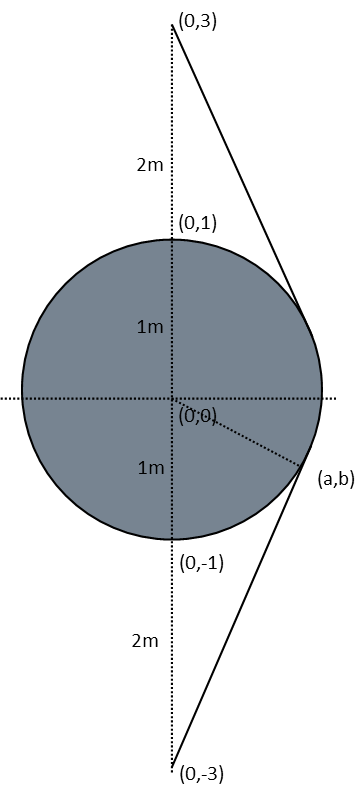
Next we must consider what it means for a line to be tangent to a circle. To do so, the line must be perpendicular to a radius of the circle. Any two lines that are perpendicular have slopes that are opposite in sign and reciprocal to each other. We can use this fact to help us find the point of tangency of one of the lines. We remind ourselves of the slope formula (rise over run), and find the slope from our point of tangency (a,b) to the origin. This is where it was convenient to label the center of the circle as the origin, because it vanishes from the slope when we plug in our points.

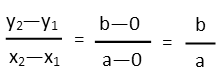
We then find the slope from the point of tangency to our speaker in the same manner. Doing this, we recognize that, since that slope is the opposite reciprocal of the slope of the radius, we set it equal to the opposite reciprocal of the slope of the radius we found, and then do some algebra to get all the b’s on one side of the equation and all the a’s on the other side.

We know recognize that this point (a,b) must also satisfy the equation of the circle. So, first, let’s remind ourselves of the center form for the equation of a circle.

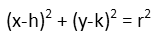
Then we express our circle using that form. Again, the convenience of placing our origin a the center of this circle crops up since (h,k) is the center, so those terms also vanish.

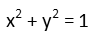
Now we plug in the point (a,b) into our circle equation. While we’re at it, let’s also get the b’s on one side of the equation and the a’s on the other.

The reason we separated the a’s and b’s on either side of the equation in both our equations is that it now lets us see that we can readily set the b sides equal to each other to solve for be, since in both cases we have just a² on its lonesome on its side. This allows us to find b (the y-coordinate of our lower point of tangency).

And now that we’ve found our y-coordinate, we plug that into either our slope equation or our circle equation (our pick) to find a, our x-coordinate. I’ll use the circle equation.

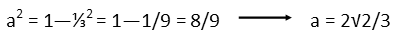
Now we have the point of tangency for one of our lines – the one from the speaker to the platform. What’s also super convenient for this situation, is that, since the outlet and speaker are equidistant from the platform, the point of tangency for the line from the outlet to the platform has an identical x-coordinate, and a y-coordinate whose only difference is its sign. It’s the SAME distance from the center of the circle, the SAME distance from the point of tangency. So the slope of its tangent line is the same. We don’t have to do several calculations again in this case. Using our reason helps save us work.

So now we have that point of tangency (2√2/3,-⅓), let’s calculate the distance from the speaker to that point. We can use the distance formula for that.

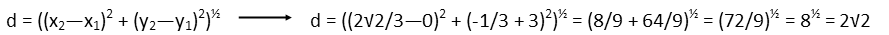
It would seem that we have now hit the tricky part – the distance of the cable following the curve of the circle. But it’s NOT. And here comes the beauty of working in radians. The length of that curve is the arc length. Radians as a measure is defined in such a way that the measure of an angle in radians EQUALS the length of the arc it describes. So all we need to do is find the central angle. Note I already drew a radius to the point of tangency so we can see an angle of half the curve of the cable. I can find that angle using any trigonometric function I want, since I know all 3 sides of the right triangle it makes. The vertical side is the y-coordinate, and the horizontal the x-coordinate, since I labelled our scale based on the measures of our distances - convenient!). I’ll pick cosine. The cosine of an angle is side adjacent that angle divided by its hypotenuse. Our hypotenuse is the radius, which is 1. More convenience, it vanishes. So our angle is the inverse cosine of the x-coordinate of the point of tangency, which means the arc length from there to the x-axis, or half the curve the cable makes, is just the inverse cosine of the x-coordinate (or a as it’s labeled in the diagram).

Now we have everything we need to find the minimum length of the cable. It’s just twice the distance from the speaker to the point of tangency (since the straight tangent line on the other side is the same length) plus twice the arc length we just found (since it’s only half of the curve the cable makes around the platform).

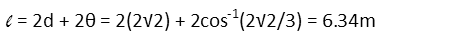
So having to go around the platform added a little bit to the length of the cable over what it would be if the platform wasn’t there, but not much. It turns out that’s because the further those outlet and speaker are from the platform, the straighter the cable will be – the platform will actually effect the length of the cable less and less – those points of tangency move further to the outside edge of the circle, closer together, making the curve around the circle shorter. Were they closer, it would add substantially more to the length of the cable since it would have to wrap around a larger portion of the platform.

When setting up a coordinate system, which we also call your frame of reference, remember to plan ahead. Make it as convenient for you as possible. So if you can make some things vanish from your math merely by how you pick your origin or your scale, absolutely do so! The more the better, because it’ll save you a lot of heartache in the long run.