Math Made Easy: Problem of the Day 76

If you don’t recognize what the question is really asking on the surface, look again. That ratio should seem familiar. Figure it out yet? It’s the definition of π. But before you make a knee-jerk reaction and say: oh, that’s just π, therefor it is 3.14159265359… ad infinitum, pause a moment. Is it? Let’s do the math and find out.

As usual, when dealing with any form of geometric problem, draw a diagram. Here, I’ve drawn a sphere with axes, and I’ve labeled an angle θ in relation to the vertical axis. I’ve also labelled the sphere’s radius a, the radius of the circle on the plane that cuts through the sphere at the circle b, and the radius of the circle on the surface of the sphere R.

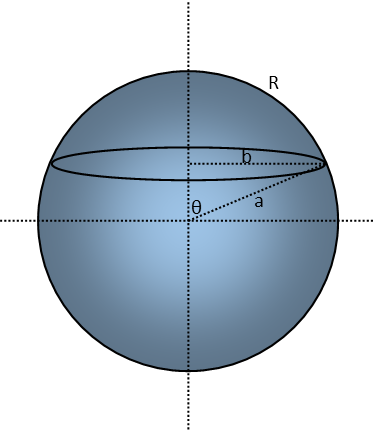
Note that as θ approaches 0, a, b, and R all approach zero. Also see that, as θ approaches π/2, b approaches a and R maximizes. This tells us we can find b by multiplying a by the sine of θ

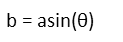
From that, we can calculate the circumference of the circle in terms of a.

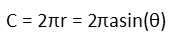
Now we can recognize the length of the circle’s radius on the sphere’s surface. It’s just the length of the arc described by angle θ, so its length is the sphere’s radius times θ’s measure in radians. This is why we should like to work in radians – arc lengths become a very simple thing to find.

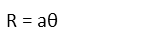
So the circle’s diameter on the sphere’s surface is twice that. This allows us to express the ratio of the circle’s circumference to its surface diameter C/D thusly:

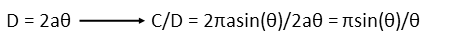
Isn’t that interesting, the radius of the sphere completely vanished. What matters most is the WHERE the circle is on the sphere.

We also see, clearly, that in spherical geometry, π is not π, at least not the way we think of it in the Euclidean Geometry of flat surfaces to which most of us are accustomed.. The ratio C/D, which defines π is NOT a constant on a sphere’s surface like it is on flat surfaces. Let’s find its maximum and minimum.

To find the maxima and minima, we set the derivative of the ratio equal to zero. So, finding the derivative:

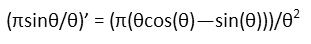
We can see that this is going to occur whenever θ times its cosine equals its sine (since that’s the only thing that’ll turn that fraction into zero). But when is that? If you punch that into a computer, you’ll find a repeating function. But our domain is restricted between 0 and π/2 (since there’s no point considering angles larger than π/2, since that just flips to the bottom hemisphere, and we may as well flip the sphere back over and treat the angle like we’re still in the top hemisphere, just to make our math easier), and most solutions given are outside that domain. So, let’s just plug in some angles close to 0.

We’ll see that this maximizes in the infinitesimal moment before our angle, and therefor a,b, and R all hit zero. And it turns out the ratio approaches the value we find for π in Euclidean space (flat space): 3.14159…

The minimum value of C/D, or π in our spherical space? 2. To find it, just plug in π/2 for θ – after that, it starts growing again.

The point of this problem was to demonstrate that π is only a constant in Euclidean geometry – that is, the geometry of flat surfaces. But once your surface picks up any curvature, π is no longer a constant. And that’s the actual universe we live in – one of curved space-time. This doesn’t mean it’s not useful to use π as a constant – we can still accomplish a lot using Euclidean Geometry in our curved space-time – heck, I did it to calculate spherical π in this problem. So don’t go throwing it out the window. It’s still a plenty useful concept.