Math Made Easy: Problem of the Day 78

Be careful when you read some word problems to make sure you understand exactly what everything is saying. In elementary school, weíre taught to focus on keywords to help us write equations. And while we do indeed need to write equations, we need to be careful not to go on autopilot, see certain words and automatically go ďA-ha! It must be this one thing, because I see *that* word!Ē Well, thatís not always the case.
Here, we see the word ďdiffer.Ē And weíre taught that differences are always subtraction. BUT. This is one thing differing from another by a certain amount. Letís say x is 4. If it differs from y by 2, then y could be EITHER 2, or 6. BOTH of those differ from 4 by 2 Ė they are both 2 away from it. 6 Ė 4 = 2, and 4 Ė 2 = 2. The way this is worded, we canít actually tell what is being subtracted from what. It could be either way. To achieve this with an equation, we can use an absolute value of a subtraction: that way, we can have two different things written in one equation. As for the second part of our problem, that really is a simple inequality, since weíre just being told to sum two different things. So we have the two inequalities below.
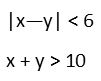
To get a better idea of whatís going on, letís rewrite all three inequalities so they appear more like lines. This is just simple algebra. Donít let the inequality sign throw you Ė treat it EXACTLY as if it were an equality, unless we change the sign on either side by multiplying or dividing by a negative number. When we do that, we flip the inequality (lesser than becomes greater than and vice versa).
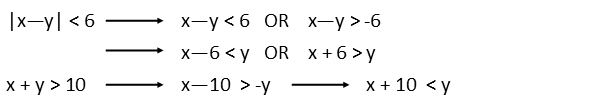
Now letís graph each of those in turn, separately, to get start getting an idea of whatís going on. When you graph an equality, graph it just like youíre doing a line. If it just less than or greater than, you draw a dotted line, if itís an equal or less (or greater) than, you draw a solid line. Thatís because the form doesnít include any point on the line while the latter does, and we need to express that in our drawing. Then you shade everything above the line if y is greater than that, and under the line if itís less.
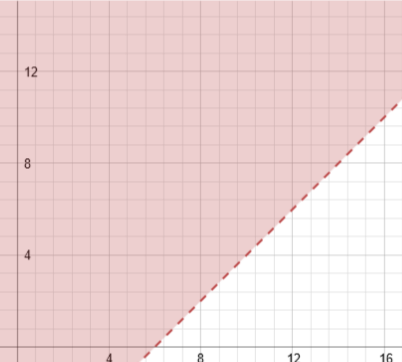
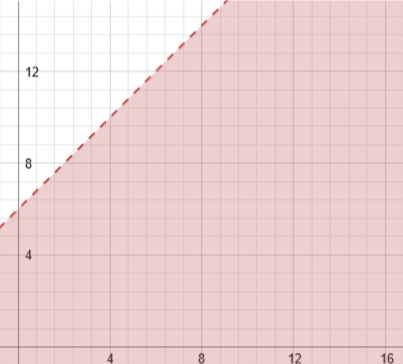
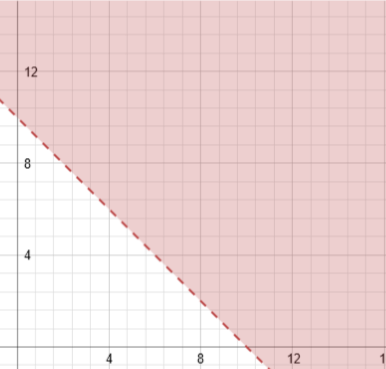
Now that we have the graphs of all three lines, we overlap them (or graph them on the same graph). We keep the shading of each line (and itís useful to use a different colour for each one, or a different shading pattern. Here Iíve used different colours). Where ALL the shading patterns/colours overlap, that is where the system of solutions exists. If it doesnít have ALL the shading, itís not part of the system Ė no input from any coordinate outside of the all-included area will work.

This gives a visual idea of whatís going on, but not clear Domain and Range. We can guess it from this, but letís actually work it out. Remember that our Domain is all possible x values, and our Range is all possible y values. Itís pretty clear we have what looks like an infinite set of each, but we still have limits.
To find this, Iím going to take the equations Iíve written, and solve them as systems of equations. When we do so, we can use elimination to find points of interest. When doing elimination, we have to make sure the inequality sign is the same in both equations, so we may have to multiply one of them by -1 to flip its inequality sign. In the first set I had to do so. For my first point of interest, I elected to solve for y, since all I had to do was add the inequalities after changing the sign of one. Doing this, then plugging that y value back into either inequality, I see a point of interest exists when x is greater than 8. This confirms what we see in our graph, because we can see that when x is greater than 8, the constraints on our y values are different than when x is less than 8.
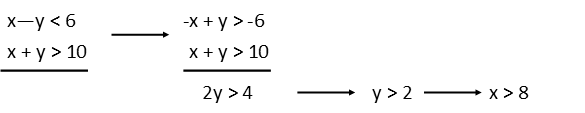
Examining first our difference inequality, we see that for both parts of the absolute value to work, y must be bigger than x Ė 6, but smaller than x + 6. Examining our sum inequality (x + y > 10), we see that any value of y within that given Range satisfies. So our Range, in the Domain (8,∞), is:
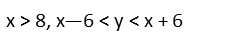
Now, solving that same system for x instead of y, since theyíre inequalities, and we may get a different result because of the possibility of the inequality sign flipping, we confirm our conjecture that x < 8 is of interest. But what is the bottom of that Domain?
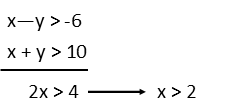
Letís set up a system using the other part of the absolute value inequality and solve it for x. We donít have to change the inequality since itís already the same, and we get to just add here to eliminate y since itís got opposite sign in each inequality. We find that thereís a point of interest when x > 2, which makes sense given our graph.
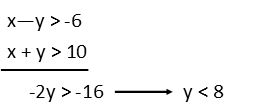
We started by examining our difference inequality for the top Domain. But looking at the graph, it looks like the sum inequality not only limits the bottom of our Domain, but the bottom of our range. So letís examine it. This inequality tells us y is always bigger than 10 Ė x. 10 Ė 2 = 8, and that falls into our happy range. If we solve the same system of inequalities for y, we confirm that, AND we confirm that y=8 is a point of interest. So we found the bottom of our Range in that Domain.
So for the Domain of 2
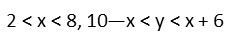
And, in our graph, we see overlap of these the upper and lower Domains and Ranges. So we know that region is included. We now know our Domains and Ranges:
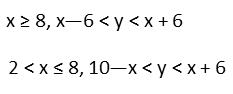
There are other ways to solve this problem, such as taking the magnitude of the absolute value rather than breaking it into two different equations, and making use of Riemann Sums. But I actually find those to be more complicated, and not taking advantage of reason. Whenever we can use our reason to find solutions rather than pounding out computations, this is desirable because it actually saves us work. Further, treating these as systems of inequalities and solving them like systems of equations to find points of interest is something that can be done on a high school level.
As always, when you have the chance to keep your math simpler, do it.
|



