Math Made Easy: Problem of the Day 79

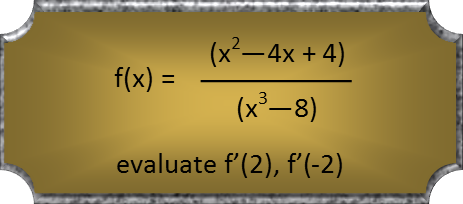
Let’s do a little bit of calculus today. And for those who don’t know how to do calculus, don’t worry, what you need here isn’t all that hard. All you really need to know are the power and quotient rules, and I’ll quickly tell you how to do them. Then you can try the problem, and continue reading if you like.

The power rule really just goes like this: take the exponent of whatever term you’re deriving, multiply the term by that, and then subtract one from the exponent. So the derivative of x³ is 3x². Constants become zero, because they effective are multiplying a variable with an exponent of zero (anything raised to the zero power is 1 by definition).

For the quotient rule, I could show you the rigorous formula for it, but I find a lot of people have trouble remembering it, or even putting it to effect. So the way I teach my students to remember it is like this: you’re going to have two terms up top, one down below. On top, your first term is the derivative of the top times whatever’s on the bottom. The second term is the derivative of the bottom times whatever’s on top. And on the bottom, you just square whatever was on the bottom before. While rigor in mathematics is good, rigorous expressions and formulae can sometimes be hard for learning students to memorize. So coming up with ways that take advantage of the human ability to visualize things, and think of things as concrete objects, can be helpful.

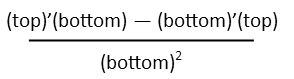
Okay, now to tackle this problem. We need to do two things before we take the derivative of our rational function: factor the top and bottom and evaluate where the Domain is restricted (in other words, where the function can’t exist because we try to divide by zero so the universe goes kablooie on us), and then simplify the function to make finding the derivative easier.

The top is just a product of squares, and the bottom a difference of cubes. So factoring we get:

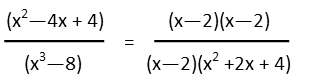
Our Domain is restricted for any value of x that gives us zero in the bottom. That’s because we can’t divide by zero, since it not only makes no sense to try to divide something into zero parts, but is physically impossible. For our function, in factored form, it’s clear that x cannot equal 2, as that’ll turn the first factor into zero. The right-hand factor on the bottom, the quadratic, however, has no real roots – this means it never crosses the x-axis is we graph it alone. Which means it can never equal zero on the real plane. Great, our only restriction to the Domain is that x cannot equal 2. The function does not exist there.

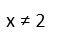
Simplifying now is easy. We see a common factor of (x-2) in the top and bottom, so we just make one go *poof* from both, leaving us with the following:

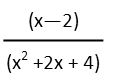
Now we can find our derivative. Remember to use the simple visualized formula I gave above. Doing that, we get:

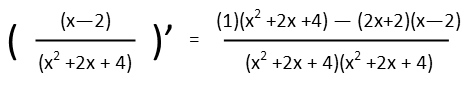
Now we just multiply everything out and collect our terms. FOIL only helps so far – with binomials. For multiplying two polynomials, it’s better to remember to just be careful, pay attention, and work one term at a time. Take the first term in the first polynomial, and distribute it to each of the terms in the second. Once you’ve done that, move on to the second term, do the same thing, then the third, etc. And a good rule of thumb to check to see if you’ve gotten everything, is multiply the number of terms in each polynomial. You should have written down that many terms if you’ve distributed everything correctly. So, for to trinomials (polynomials with three terms) multiplied by each other, as we have in our denominator, you should have written down 9 total terms (3x3=9).

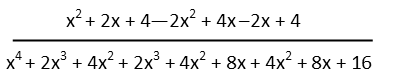
Once we have everything distributed and multiplied, we can go ahead and collect our terms to simplify everything.

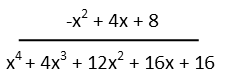
With that done, we have our general derivative. Our problem asks us to evaluate it in two places. We don’t actually have to do both, though! Since the function doesn’t exist at x=2, the derivative doesn’t exist (if you plug it in here, you’ll actually get a sensible value of 1/12, BUT, there’s no point evaluating a derivative where a function doesn’t exist). So we really only have to evaluate f’(-2). To do that, we just plug -2 into every spot we see an x in our derivative. The rest is just simple math.

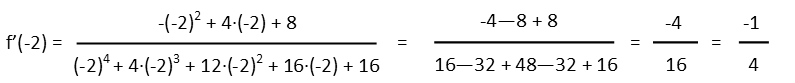
We see our derivative at -2 is -¼. This tells us that our function is decreasing here. But, for the purposes of this problem, we’re done for the day.

If we think of ways to see parts of our problems like objects, like building blocks, and remember certain formulae or rules in ways that we’re just manipulating those objects, it really can make our math a lot easier. The Quotient Rule of Derivatives is one of those times. See if you can find other places in math where doing so helps you.