Math Made Easy: Problem of the Day 80

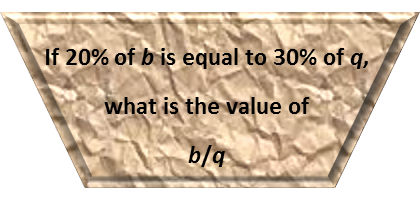
It looks like we have a fractions revisit today. There are two different ways to approach this problem, and both end up producing fractions. Which shouldn’t be surprising since we’re asked to evaluate one in the question.

When we see problems with two variables, we must remember that we may be able to answer the question without finding the variables. In this case, we don’t have enough information to find them, but, since we’re being asked the value of their ratio, we can most certainly answer the problem. All we have to do is relate them and do a little algebra until we’ve produced something that looks like their ratio.

Let’s first treat it like a problem entirely in fractions. I recommend doing this as much as you can since fractions are much easier to manipulate than decimals. The fractional equivalent of 20% is 1/5, and the fractional equivalent of 30% is 3/10. So, given the condition provided, we can set up the equation as follows.

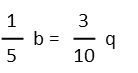
Now we just want to move things around until we have b/q on one side, and everything else on the other. Let’s move the 1/5 first. To do that, we need to cancel it out on the left side, and do the same thing to the right (because whatever we do to one side of an equation, we must do to the other side). Multiplying both sides by 5/1 will do quite nicely.

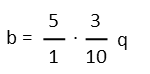
Simplify before we multiply! We see that the five cancels, and the 10 reduces to 2.

Now we just move the q. To do that, we divide both sides by it, giving us our desired b/q fraction on the left and nothing but a constant on the right. We’ve found our value for b/q.

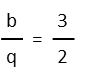
Let’s do that another way. If we write the equation in decimal equivalents, we get:

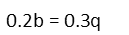
To eliminate the decimals, we can multiply both sides of the equation by 10. Effectively, this just moves the decimal one place to the right for both decimals.

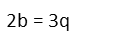
Now moving the 2 by dividing both sides of the equation by 2:

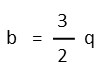
Finally, we move the q by dividing both sides of the equation by the same, giving us the same result we got treating the problem entirely as fractions.

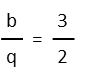
Just a little bit of algebra, remembering all you’re really doing is moving things around, and problems like todays are easily solvable. I like staying in fractions as long as I can, but for this one, the decimal equivalent way wasn’t that much more difficult, and it became fractional quickly enough. Choose what works best for you.