Math Made Easy: Problem of the Day 81

Working with radicals is never pretty. It generally uglies up math, and it tends to make people forget their exponent rules. It’s almost always better to use exponential notation, which allows us to see that roots and powers are a continuum of the same thing, and that the math works the same for both. So in that light, let’s first rewrite today’s problem in exponential notation. Remembering that a root is the bottom of the fraction in exponential notation, we get:

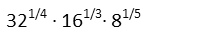
Now that we have them expressed as exponentials, we recognize we cannot apply the product rule (since we’re multiply all of our terms) until we give them a common base. We can see that all three bases are powers of two, so we write them as a power of 2 (32 is 2⁵, 16 is 2⁴, and 8 is 2³), and put that power in the top of the exponent.

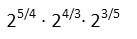
With them having common bases, we can apply the product rule. That tells us to simply add the exponents. I’ll do that as some separate math, treating them as their own fractions, so I get:

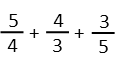
Let’s add the first two, giving them a common denominator.

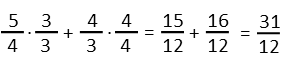
Now that sum plus the third, giving them a common denominator:

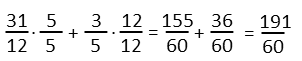
This gives us a really ugly looking exponent.

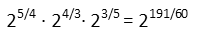
BUT, we can actually almost evaluate this in our head, even though the fractional exponent is not simplifiable. 191/60 is a little over 3. So our result is a bit bigger than 2³ but smaller than 2⁴. And since it’s 11/60ths over 3, that means it’s about 1/6th of the way between 2³ and 2⁴, so about 1/6th of the way between 8 and 16. That puts it a little over 9. Putting our result into a calculator to confirm, we get 9.08. So our educated estimate was pretty good.