Math Made Easy: Problem of the Day 82

We don’t need to know the radii of any of these circles to solve this problem. We’re given enough information in the wording. If each is larger by the next by the diameter of the inner circle, than we can simply assign a variable to the radius of the inner circle and express each circle’s radius from that. First, let’s draw a diagram of just the first three concentric circles, and label the radius of the first. I’ll also label the distance from the edge of the inner circle to the edge of the second, and from there to the third.

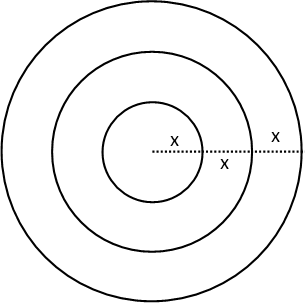
Note that all three distances are the same. If the second circle is one diameter bigger than the inner, then its radius is one radius bigger, since the radius is just half the diameter. It’s a direct proportion. That makes the third circle one inner radius bigger than the second. So each ring is exactly one radius thick. We don’t need to diagram all six circles to see the pattern. Those three were sufficient. Now we can start calculating the areas of the inner circle and each ring, which we need to do if we’re to find how much more paint we need to cover the purple rings than the black areas.

The inner circle is easy. We just remember the formula for the area of a circle and plug in our variable for r. Though, honestly, we didn’t even need a variable. We just could have used r, if we so wished.

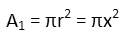
The area of the second ring is going to be the area of its circle minus the area of the inner circle. So for it, we get:

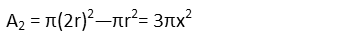
And for the third ring, we subtract the area of the second circle from the area of the third circle. We do similar for all the remaining rings, so we should get something like this:

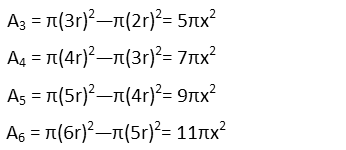
To find the area of the black paint, we simply add the areas of the inner circle and rings 3 and 5. To find the area of the purple, we add the areas of rings 2, 4, and 6.

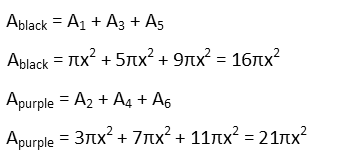
Now that we know the areas of purple and black paint, to find out how much more purple paint we need than black, we set it up as a ratio of purple over black, and simplify. Nicely, our variable cancels itself, as does π. We get a simply fraction, which we can convert to a decimal, or a percent if we like. And this tells us we need about 31% more purple paint than black (since the percent is over 100, we know it’s more, and we just drop the 1 to tell us the percent more).

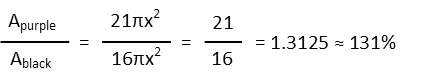
Remember: Draw your diagram, break your problem into parts, and attack each part one at a time. This will make most problems simple.