Math Made Easy: Problem of the Day 83

My normal advice is to always diagram the situation for every math problem you do. But, with this one, hectagon being a one hundred sided figured, that might prove quite difficult. In fact, as a polygon gains sides, the more approximately it appears to be a circle. A hectagon has a LOT of sides, and is very similar in appearance to a circle because of that. So drawing this might not be the easiest thing in the world. BUT, we *can* still draw a useful diagram, and the hint to that is in the setup.

Just as in the setup, I drew two octagons instead of two hectagons, you can do the same. Just pick two polygons you *can* draw, and do the diagram with them instead of hectagons. It will actually prove useful. When doing the diagram, let’s make sure to extend two rays from one of the polygon’s sides so that we can clearly see the exterior angles. Note that the exterior angles are those made by the side of the polygon and one of the rays. NOT by the outside of the two rays. When we do this, we can see that the angle we’re asked to measure is made up of one exterior angle from one of the hectagons, and one from the other. So now we’re ready to do our math.

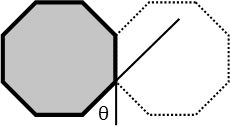
We know that the sum of all the exterior angles of any polygon is 2π radians (or 360 degrees), so each of those exterior angles has a measure of:

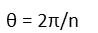
Since the angle we want is made up of two of them, we just double both sides of the equation:

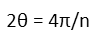
And then we plug in our number of sides, 100:

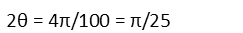
Simple enough. We could also have solved it by finding the interior angles, and recognizing that those exterior angles are supplementary. We talked about interior angles and the formula for finding those in Problem of the Day 36.

If we wanted the measure of that angle in degrees, we’d just replace 2π with 360:

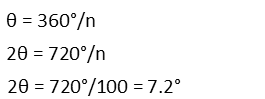
That angle is pretty small, and that’s what we should expect from a figure with so many sides.

The technique we used for our drawing is called approximation, and it’s actually a pretty useful technique – it’s part of how calculus was derived, and physicists use it all the time to help approach answers for very difficult problems. Sometimes a quick approximation helps you see the more complex picture, and makes what seemed like a difficult problem turn into a cake walk.