Math Made Easy: Problem of the Day 84

While drawing a picture might be useful for today’s problem, it’s not really necessary, and might actually take more time to do than figuring out the algebra behind the problem. For ones like this, it’s usually best to contemplate the wording of the question and try to come up with as many equations as you can, and then go from there.

To start, let’s assign a variable. You can assign one to any of the people, and then write equations relating each to that variable, or assign a variable to the total number of eggs. I prefer the latter for this problem, so I’ll do that. Then writing the equations is just a matter of relating each person to that variable. Sylvia’s is the easiest since the question directly relates her number of eggs to the total, so let’s do hers first.

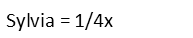
Leroy’s is just a fraction of hers, so I’ll multiply hers by that fraction to get his portion of the total.

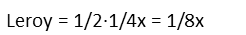
For Lees, I just add six to Leroy’s.

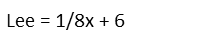
Angus’s is half that, so I multiply Lee’s total by ½.

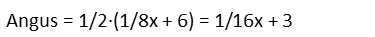
Margaret’s being three times that, multiply Angus’s expression by 3.

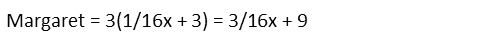
Now that I have an expression for all five students, I simply add them all together and set them equal to our variable x.

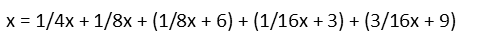
Dropping the parentheses and adding the constants, we get.

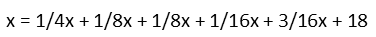
Now let’s give all those fractions a common denominator so we can add them.

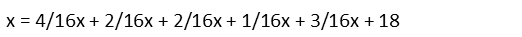
Once we’ve added them, we can move the x from the right-hand side to the left by subtracting it from both sides, and simplify.

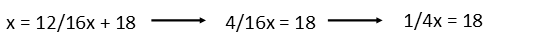
After which we multiply both sides by the reciprocal of the coefficient of x, and we have our answer: there are 72 total eggs.

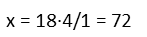
Keep it simple. When you can’t draw a picture, formulate expressions and equations. By the time you get done doing so, the problem may have solved itself.