Math Made Easy: Problem of the Day 85

We’ve got an incoming case of conjugates! When adding fractions, we always need to find a common denominator. But the fractions in today’s problem are all irrational, so let’s rationalize them *before* we find a common denominator. We want to do that because we’ll have to rationalize eventually, anyway, and if we find the common denominator *before* we rationalize, we’re probably going to make rationalizing an absolute pain, especially since our complex numbers in the denominators involve imaginary components and root components. We might also find that, after rationalizing, we no longer need to find a common denominator – that part might work itself out.

Let’s rationalize one fraction at a time to make our lives easier.

To rationalize any complex number, we multiply by the version of one that involves the conjugate of the denominator. We like multiplying by different versions of 1 because it doesn’t change the value of our term, but it does change its appearance, which is useful. Finding the conjugate of a complex number is easy – just change the sign in the middle. So, multiply top and bottom by the conjugate of (3 – 2i), we get.

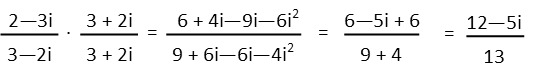
Note that I wrote out all the terms when we distribute correctly, even though I knew the middle terms in the denominator would cancel. I did that just to demonstrate how multiplying by the conjugate eliminates the imaginary component. Also recognize that i² is -1, so the squared term becomes a real number.

For a binomial with a root in one term, we do exactly the same thing – multiply top and bottom by the conjugate of the denominator. The conjugate for that is also found simply by changing the sign in the middle. See how the root terms in the middle of the denominator also cancel each other out, and a square root times a square root turns into an integer.

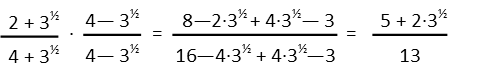
We repeat the process for the second two fractions, using exactly the same techniques.

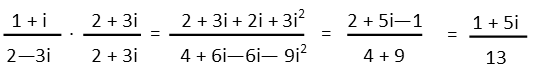
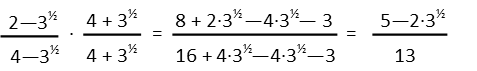
Finally, we put everything back together. Isn’t it convenient that all these fractions ended up with the same denominator? That saves us further work in finding a common denominator. All we have to do now is add all the numerators. And, in our case, we also seem to have the convenient happenstance that the imaginary terms cancel as well as the root terms. So our original expression was just a really fancy and complicated way of writing the fraction of the two prime numbers 23/13. At this point, if we could, we would like to simplify, but since those numbers are both prime, we’re done.

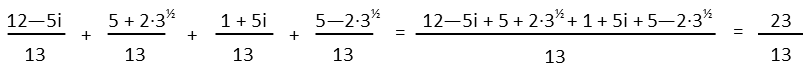
Remember, when adding or subtracting complex numbers, or fractions with roots in the denominator, rationalize FIRST. It will almost always save you some headache in the long run.