Math Made Easy: Problem of the Day 86

The slope of a line tangent to a curve is the derivative of that curve. With any curve, this clearly changes, which is why the derivative of anything but a straight line gives us another expression with a variable in it. That’s okay, to evaluate it at any given point, we just plug in the value of the axis-coordinate with respect to which we took the derivative (usually, and in this case, the x-coordinate).

Just as with simpler (and more complex) math, we want to simplify our equations and expressions as much as we can before we start manipulating them. This will save us headache in the long run, and will get us the same results. We could, if we wanted to, take the derivative of our curve right off, but it could be a pain – we have a product, a square, and a quotient, so we’d have to apply all three rules of derivatives all at once. If we simplify, we might reduce the work we need to do. So let’s do that. Factoring the top and bottom, we readily see that we can cancel out a factor of x and (x – 2) from both the numerator and denominator.

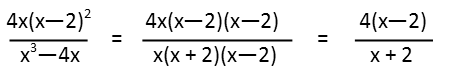
That made our expression much simpler, and our task much easier. Before we apply our derivative, let’s make sure our expression actually crosses the x-axis. We know that when we have a rational function who’s numerator and denominator have equal degree, there exists a horizontal asymptote at a point where y is the ratio of the leading coefficients. So, for this expression, there is a horizontal asymptote at y = 4. And since our function has a degree of 1, we know it crosses the x-axis – since it’s an odd degree and positive, it starts way down at negative infinity on the left and goes way up to positive infinity on the right. We also need to consider whether the function exists at the x-intercept. The function does not exist at any value of x that makes the denominator zero. Looking at the factored version of our expression, we see that there are three places where this occurs: -2, 0, and 2. At x = -2, we have a vertical asymptote, since that factor exists only in the denominator. At x = 0 and x = 2, we have holes, since those factors exist in both the numerator and denominator (a hole just means the functions skips that point as if it weren’t there).

It’s time to calculate the x-intercept. Since that’s where the curve crosses the x-axis, we know that y=0 at that point. So we set our expression equal to zero and solve for x. We can ignore the denominator when doing this, since we can’t divide by zero. Anything that makes the numerator zero, but not the denominator is where our function crosses the x-axis, so long as the function exists there.

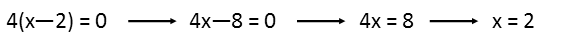
Well, look at that. The x-intercept is at one of our holes. The function doesn’t exist at that point, therefore the derivative does not exist at that point. So we're actually done at this point in time.

But let’s calculate the slope of the line tangent to that point, anyway, just for practice. Just remember it doesn’t actually touch the curve since the point of tangency doesn’t exist on the curve. All we have to do is apply the quotient rule of derivatives. Remember from Problem of the Day 79 that it looks like this:

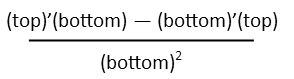
So, applying that to take the derivative of our curve, we get the following. Note that I distributed the 4 in the numerator for ease of derivation.

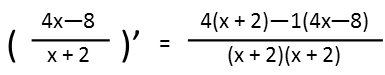
Distributing the coefficients in the numerator and rewriting the denominator as a square, we can then collect the terms in the numerator. It’s convenient that the x terms in the numerator both cancelled each other.

With that, we plug in the x-coordinate of the x-intercept, and simplify.

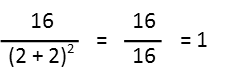
So, if our curve actually existed at that point – if it were just the simplified version of the rational function rather than the given form – the tangent line would have a slope of one. The graph of the two (ignoring the holes on the curve) looks like this:

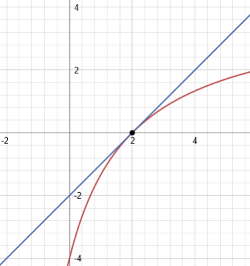
Remember to always simplify your expressions and evaluate the restricting values of the function before manipulating. You’ll save yourself a lot of work if you do so.