Math Made Easy: Problem of the Day 87

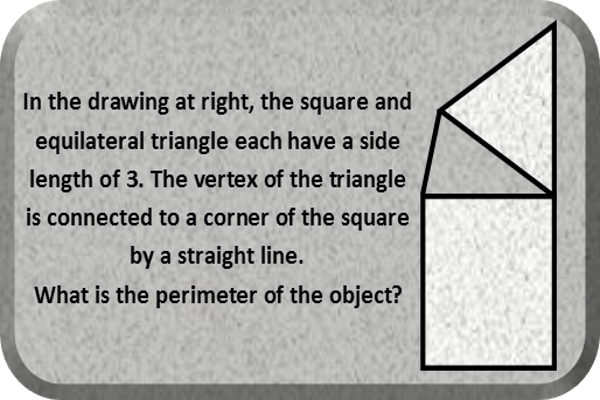
A short one for today. As always, when you can draw a picture, do it! When we draw our diagram for this instance, we recognize that we can label the sides of every figure in it except one – the connecting line, which makes the short side of an isosceles triangle. We have two sides of that triangle, so if we know the angle included between those two sides, we can use the Law of Cosines to find the short side. We also know the measure of all the angle of the square - π/2 – and the equilateral triangle - π/3 – so we can label the angles on either side of the included angle.

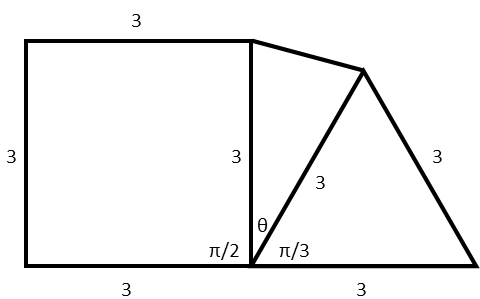
The included angle is supplementary to one of the angles of the equilateral triangle and one of the angles of the square – their total measure is π. So to find it, we simply subtract from π one angle of the square and one angle of the equilateral triangle.

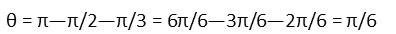
With that measure, we can remind ourselves of the form of the Law of Cosines:

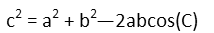
Now we plug everything in and solve for that short side. We know that the cosine of π/6 is 3^½ from our unit circle. When we finish all our addition, subtraction, multiplication, and roots, we find our answer to be just slightly over 2, so let’s just round off to the nearest whole number.

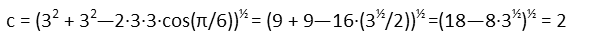
The perimeter of the object contains 3 sides of the square and 2 sides of the equilateral triangle plus the short side. So to find it, we simply multiply the given side length by (3 + 2) = 5, and add the short side we found.

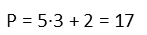
This gives us a perimeter of 17 units. We could also find the area of the figure if we like. Do that as an added challenge.