Math Made Easy: Problem of the Day 88

Since we’ve done a couple derivation problems involving the quotient rule, I thought I’d do another derivative problem, this time involving the chain rule. It applies whenever we take a derivative of a function with another function inside it, and is generally used to make such functions easier to do, saving us the time of working out those functions before taking our derivative. So let’s first remind ourselves of the chain rule, and try to do it in a way that is more visually intuitive than in rigorous mathematical notation. I like to teach it to my students like this:

It basically means, take the derivative of the outside function without touching the inside. Then multiply that by the derivative of the inside function.

But before we go blindly applying the chain rule to this set of functions, let’s carefully look at what we’re being asked to do. If we were asked to take ONE derivative, ie d/dx (f(g(h(x))), the chain rule would absolutely apply and be the way to go – we could compose our functions, and just work the chain rule. BUT. That’s not what we’re being asked here. The notation of what we’re being asked to find reads: find the derivative of the function f including the derivative of the function g including the derivative of the function h. To do this, we’re really going to need to work from the inside out. We have to take the derivie of the function h, plug that into the function g, then take the derivative of the new function g, then plug *that* into the function f and take the derivative of *that* resulting function. What we have here is not the derivative of a composite function, but a composite derivative. This may result in multiple uses of the chain rule.

So let’s first take the derivative of function h. That looks pretty simple. No functions inside functions, just two being added together (a fourth power and square function), which means we take their derivatives separately and add.

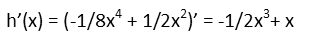
Now we plug that result into g(x) wherever we see an x in g(x).

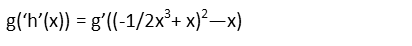
We see we DO need to make use of the chain rule here. We have a cubic inside a square function. It’ll be much easier to take advantage of the chain rule than multiply these out and derive. Doing that, we still have to multiply to binomials, but it’s not too bad. Just make sure we distribute everything correctly.

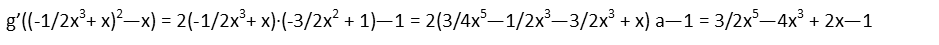
Plugging that into f(x), we get:

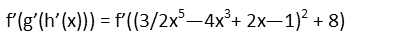
Again, we need the chain rule to take this derivative. Make sure we’re careful about writing everything down correctly. Remember that we don’t touch the insides when we take the derivative of the outside.

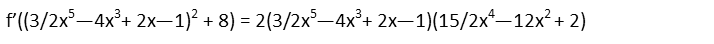
The rest is distribution and careful accounting for terms. Let’s multiply out the two polynomials first. I usually lie to pick the one with the fewer number of terms and make sure I distribute each of its to the one with the larger number, as I find it easier to not lose track of what I’m doing that way. A check to make sure you have the correct number of terms, is to count the number of terms in each polynomial and multiply those figures – you should have that many terms when you’ve correctly distributed everything. For instance, with these two polynomials we have the first one with 4 terms, the second with 3. So we should have 4x3 = 12 total terms before we consolidate everything.

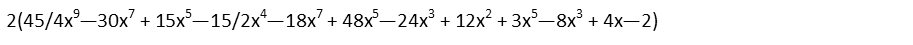
And that’s what we got. Now, let’s consolidate all the like terms. So we look for terms with the same variables and exponents, and add them.

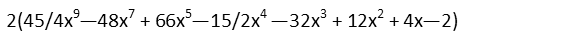
Finally, we distribute that 2 to all the inside terms.

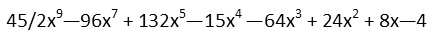
If we want, we can write it in factored form, but expanded form is good for now.

For an added challenge, factor the expanded polynomial, and find all the physical meanings this derivative tells us about this particular function.