Math Made Easy: Problem of the Day 89

I normally like to see if a problem involving area can be solved geometrically, or with trigonometry, before I go the calculus route. At least when I’m demonstrating problems, since it helps reinforce a lot of the concepts that go into calculus and engages the visual and tactile parts of our brains. Let’s graph these two functions, and see what the overlap looks like to see if we can devise a geometric approach first.

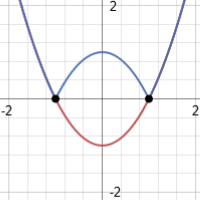
The enclosed area looks kind of like a fat football. No immediate geometric devices come to mind for solving this, so let’s go the calculus route. The area under a curve can be found by computing what we call the definite integral – integrate the curve and evaluate it within a given range. To find an area enclosed by two curves, you can simply just integrate both and either add or subtract, as is needed. Here, we see that we need to add the areas (since when we calculate the definite integral it’ll give the area between each curve and the x-axis). That hump is created by the absolute value function, and looks a lot like the opposite function of x² - 1, which would be –x² + 1, so let’s graph that on top of everything and see if that supposition is correct.

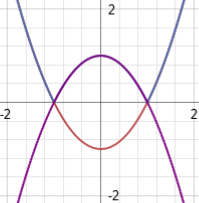
Well, look at that, it is. So instead of trying to integrate an absolute value, I’ll just integrate that opposite function instead.

Let’s start by computing the definite integral of the first function. Remember an integral is just a backwards derivative, so it’s really asking: “What function, when derived, gives us this function?” So finding the indefinite integral for our first function, we get:

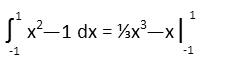
I picked the domain of -1 to 1 not just because that appears to be where we overlap on the graph, but because we can clearly see that both function are identical until the first one becomes negative. It is negative only in the very limited domain of -1 to 1. So that’s where we’re evaluating. To do so, we simply plug the number on top of our range into our integral, find what that is, then plug the number at the bottom of our range into the integral and subtract the resulting value from that. Usually we do it all at once, so we get something like (upper bound evaluation) – (lower bound evaluation). For our first function, we get the following:

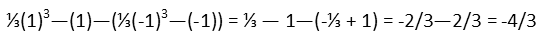
Now we compute the indefinite integral of our opposite function:

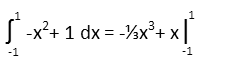
And we evaluate that over the same domain.

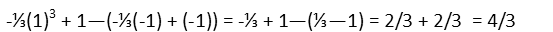
When we add the areas, we recognize that though the first function gave us a negative area, we really want that to be positive. It contributes to the enclosed area and doesn’t take away from it. It’s okay that its area was evaluated as negative initially, because that just tells us which side of the x-axis it’s on. It’s up to us with our big human brains to recognize we really need to make it positive when we’re totaling our areas.

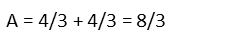
And there we have our answer. The area enclosed by the two curves is 8/3 square units (or 2 ⅓ square units).