Math Made Easy: Problem of the Day 90

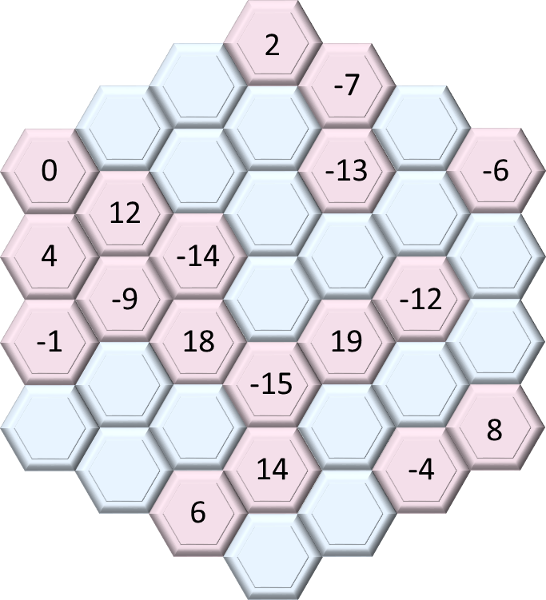
Time for another number puzzle, hooray! Hexagonal number grid puzzles are a bit trickier than square ones. There are more paths the numbers can take, so more patterns to look for. It can still sometimes help to try to set up expressions for a sequence when you can, but first you really need to find the path patterns. Once you find those, finding the sequence that solves the puzzle should be easier.

Also remember that, when solving a number puzzle, there may be more than one sequence involved in solving it. Our first one way back on Problem of the Day 34 was a case of that. So we need to keep that in mind when we’re looking for our pattern.

So let’s look for vertical patterns first. Going down the left-hand column, we see an increase of 4 than a decrease of 5. If we try to apply that to the next column over, it doesn’t work. -9 is 21 smaller than 12, not 5. And the next column the difference is even bigger. So that doesn’t seem like it’s going to work.

Going horizontally, and keeping in mind there are different ways to go horizontally on a hexagonal grid, we see that patterns fail to emerge no matter how we make our horizontal moves (zigzagging or skipping to the next exactly horizontal cell). But one kind of pattern you can readily do on a hexagonal grid, much more easily than on a square, is a spiral. You can do them on a square grid if you set them up correctly, but hexagonal grids almost beg for a spiral pattern to be used. So let’s look for one here.

A spiral always has a first cell and a last cell. The center cell is always either the first or last. On the outside, we’re not sure where to start – which cell could have been the first one? So, when looking for a spiral pattern, it’s best to start on the inside. Keeping that in mind, let’s look for a spiral going from the central cell to the outer.

If you follow those negative numbers, it looks like a spiral actually does emerge – follow the -15 to the -14, than the -13, than the -12, and you can see a definite spiral starting to form. One that’s got a counting up as you go out from the center. And the two positive number, 19 and 18, might even be part of it, but they’re counting DOWN as you go out from center, if we keep them on the same spiral. If we project outward, that holds with the 0 and -1, spaced one cell apart, counting up, as with the -7 and -6.

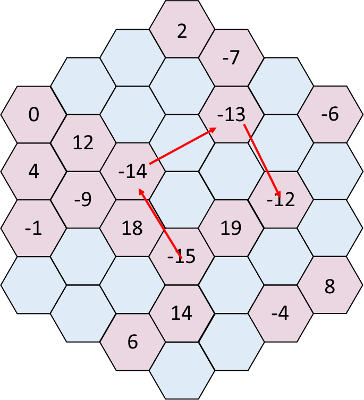
So it looks like the pattern is found. It’s a spiral of two sequences, one counting up, one counting down, going out from center. As there are only two cells left after 19, following the spiral, and the next one after it must be -16, the inner cell must be 20.

So our solution looks like this:

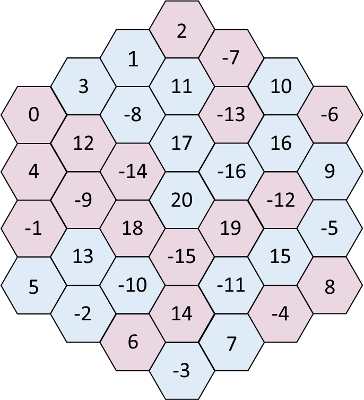
I hope you enjoyed this puzzle!