Math Made Easy: Problem of the Day 91

I like presenting real-world situations like this because they quite elegantly display how you really do need to pay attention in math class and not just brain dump it all after every exam. If the painter shows up to the job without enough paint, he’s going to waste time having to go buy more, and possibly miss his deadline. If he shows up with too much, he may wind up with excess paint he can’t use elsewhere – perhaps the colours needed were specialized and none of his other clients will use anything similar. So it’s in his best interest to calculate just the right amount of paint he needs beforehand.

Fortunately for our painter, the areas here are easy to calculate. The only difficulty is that he’s only given one measure, and the others are all relationships. He can easily calculate the area of the small square and triangle without needing to find any other sides, but for the large squares and triangles, he needs to find those side lengths first. So let’s find all the side lengths before we bother with areas.

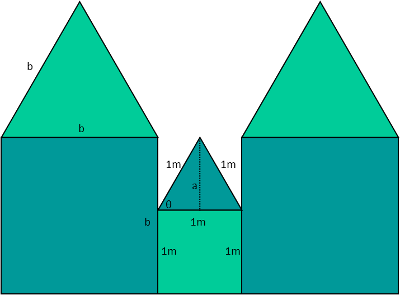
To get the side length of the big squares, we need to find the height of the small triangle. That’s because the big square’s side length is just the side length of the small square plus the height of the small triangle. If we draw a new diagram and label everything we know and need, we see that we can readily calculate the height of that small triangle using the sine function. It is opposite a known angle – θ is π/3 radians since the triangle is equilateral – and forms part of a right triangle. We remind ourselves of the definition of sine in terms of the sides of a right triangle, plug in a and 1 for the length of the hypotenuse (since it’s an equilateral triangle and it’s bottom side is the same as the small square as it’s a shared side, the hypotenuse of the right triangle is also the same as that shared side). It’s convenient the hypotenuse had a length of 1 meter, because it basically just drops out.

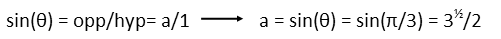
Now that we have that height, we find the side length of the large triangle by just adding it to the side length of the small square.

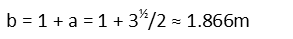
And that’s actually everything we need. Note in the diagram I labelled the sides of one of the big equilateral triangles as b for the same reason the small triangle had the same side lengths as the small square.

Now for the areas. Here’s another diagram labelling the four areas we need to find. I labelled the small square A, the big square B, the small triangle C, and the big triangle D.

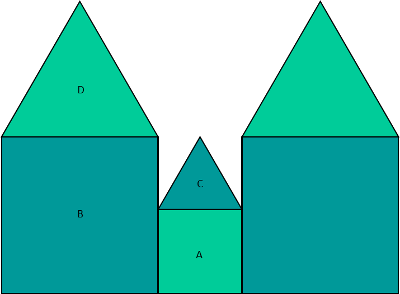
The area of A is easy – just square the side length. And 1² is just 1. For B, the big triangle, we just square its side lengths, as well.

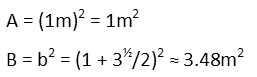
For C and D, we remind ourselves of the general formula for the area of a triangle. For C, the angle is π/2, and the sine of that is just 1, so it effectively goes away (no need to write that down since multiplying by 1 doesn’t change anything). For D, the angle θ is again π/3 since it’s an equilateral triangle.

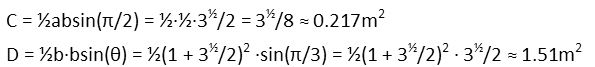
Now that we have those four areas, we finish our calculations for how much paint he has. The blue green paint area is made up of the two big squares and the small triangle, so is 2B + C. The Caribbean green area is 2 big triangles and the small square, so 2D + A.

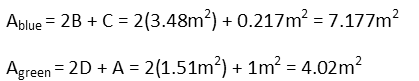
And since he has to buy only whole cans of paint, he needs 8 buckets of blue green and 5 of Caribbean green. Calculating this ahead of time will save the painter money in the long run, as well as time. Knowing your math really is necessary in the “real” world.