Math Made Easy: Problem of the Day 92

While I’ve covered a little bit of calculus in our Problems of the Day, I haven’t yet really touched much on vectors. Today’s problem can be solved through trigonometry, but it’s best solved using the dot product. As we add dimensions and directions to our mathematics, it can quickly become clear that we need different ways of multiplying multi-dimensional objects, especially those with a direction. The dot product is one of those ways, and we can garner physical information from vector through manipulation of it. One of those pieces of information is the angle made between two vectors.

To use the dot product to find that angle, we can use the following formula (found by Gibbs et al around the turn of the 19th Century):

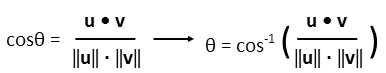
The formula directly relates the cosine of the angle to the dot product, with an inverse relation to the magnitudes of the vectors involved. Note that I took the extra step to take the inverse of the cosine on both sides so we can directly solve for our angle θ. To explain a couple things in notation: vectors we usually express as an emboldened variable. The dot product operator is expressed as a heavy emboldened dot to differentiate it from the light dot of the simple multiplication operator. The double bars around a vector mean to take the magnitude of that vector.

Let’s break it down and do each piece in steps. To find a dot product, we simply multiply the like components of each vector, and add all the products (note that if our vectors are one dimensional, they only have one component each, and so the multiplication you learned in elementary school is just the one-dimensional case of the dot product, thus the shared word “product”). In general form, it looks like this, where we define our vectors as :

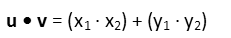
So plugging our components in, we find the dot product of these two vectors to be:

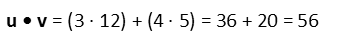
To find the magnitude of a vector, we simply use the Pythagorean Theorem, since, if we draw the vector starting at the origin, we can make a right triangle where the vertical component is one leg and the horizontal another, with the vector itself being the hypotenuse:

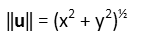
Applying that to our first vector, we get:

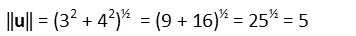
And to our second:

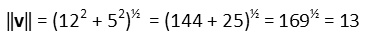
Now we can just plug everything into our first formula for the angle, giving us a result of 0.53 radians (or about 30.5 degrees).

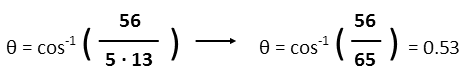
An interesting consequence of the cosine being directly related to the dot product, is that, were our angles perpendicular, or at an angle of π/2 (90 degrees), their dot product would be zero. A better word for this is orthogonal – anything that is orthogonal to something else is perpendicular to it in all respects, or has a dot product of zero.