Math Made Easy: Problem of the Day 93

It’s always good to get practice simplifying fractions, and that’s really all today’s problem is. The exponents are just there to make it look a little bit different, but, really, all they do is break up the integers that they represent.

Let’s start this one by changing those negative exponents to positive. We can do that by simply moving each term with a negative exponent to the other part of the fraction. So the 15^-3 moves to the bottom and the 4^-2 moves to the top. Both of their exponents become positive when we do that.

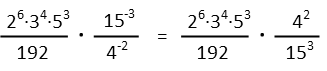
I see that in the numerator of the first fraction, we have one exponential term with a base of 3, another with 5, and recognize that these are the factors of 15, which is the base of an exponential term in the right-hand denominator. So I’ll factor a 3 out and take advantage of the associative property to regroup those two terms in the left-hand numerator. Then I’ll multiply the bases, which I can do now that they have a common exponent.

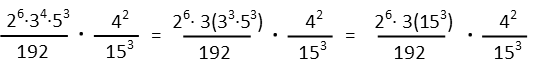
That gave me a 15^{3 in one numerator, and one in a denominator. So I can cancel those terms now.}

I could give the exponential terms with bases of 2 and 4 a common base if I wanted to do so, right now, but I still have that 192 in a denominator, and I think it’ll be convenient to leave those exponentials as they are at the moment, so instead, I’ll tree-factor that 192 so I can see what exponentials I might have hiding inside it.

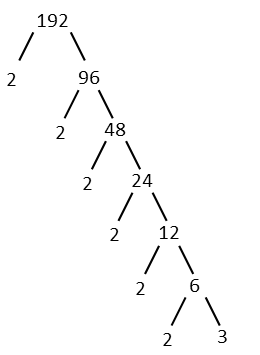
When we get done doing that, we see we have 6 twos and one 3. Six 2s in the factor tree is just 2⁶. Oh, fantastic! That means the numerator of that fraction and the denominator are the same thing. We can just cancel the top and bottom of the left-hand fraction. It equals 1. That leaves us with just 4² to evaluate, which is easy. Our simplest form of our starting fractions is just the integer 16.

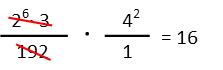
My strategy when I simplify fractions is almost always to avoid doing any multiplication that I don’t have to do. So if I have terms broken up like we did here, I leave them that way until I can no longer cancel terms. This can make problems much easier, and saves me from having to undo work I did earlier – if I multiply at any time before I’ve fully simplified, I just have to undo that when I continue simplifying. Why cause yourself more work than you need to do?