Math Made Easy: Problem of the Day 95

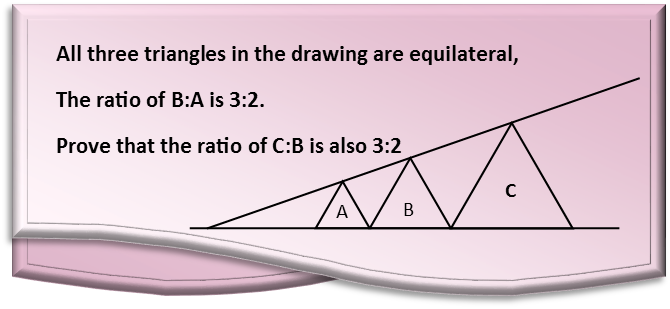
Mathematical proofs always present interesting problems. They test your knowledge of mathematics as well as geometric relationships. For many, there are multiple ways to go about proving the assertion. Today’s problem is no different – there are definitely more ways than one to do it.

I’ll go about by proving the statement by finding the equation of the line that touches on each triangle’s vertex. I’ll then find an expression for the height of Triangle C, and use that and the line equation to find the base of Triangle C. Once I have that, it’ll be simple to compare the two ratios.

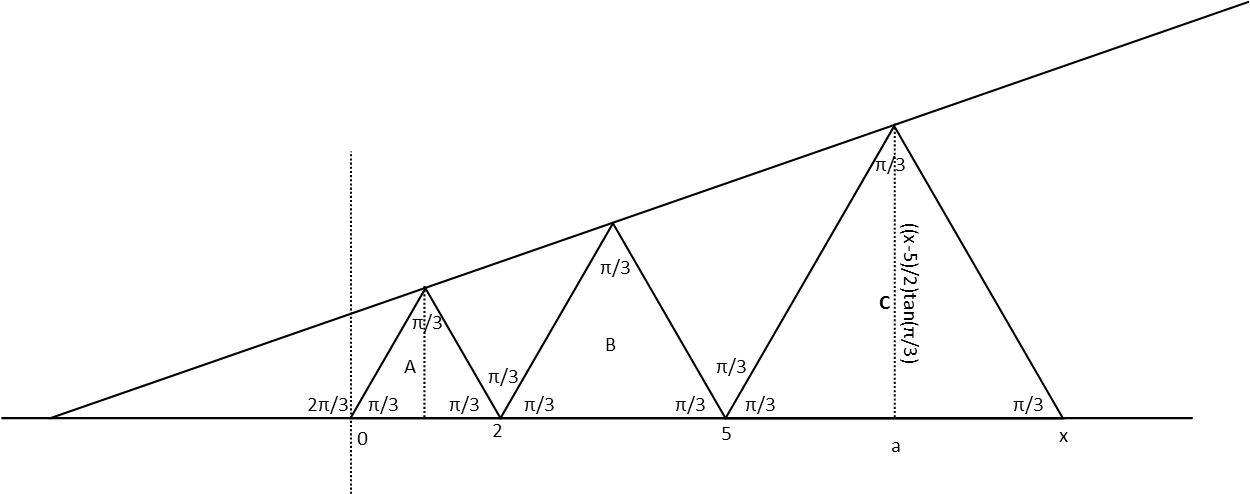
As always, let’s start by diagramming the situation. Your diagram will frequently be dictated by the strategy you plan to use to tackle your problem. For this one, I’ll set the origin at the left-hand base of Triangle A. Since the ratio of B:A is 3:2, the ratio of their bases is the same. So I’ll arbitrarily assign a length of 2 to Triangle A’s base. This means Triangle B has a base of 3. So, in our coordinate system, the right-hand point of Triangle A is at the x-coordinate 2, and the right-hand point of Triangle B is at the x-coordinate 2+3=5. I’ll label the right-hand point of Triangle C as x, label the midpoint of Triangle C’s base as a, and label what angles I easily can.

Now to find the slope of the line. Remember the we find the slope of a line with the rise over the run.

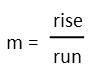
The rise of the line is just the difference in the heights of the triangles.

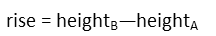
The height of Triangle A we can find by recognize it forms a right triangle whose base is half that of Triangle A. Since the height is opposite a known angle, and the base adjacent, we can use the tangent to find the height (opposite/adjacent). This means the height is equal to the tangent of the angle times the adjacent side, which has a length of 1 (since it’s half of 2). For Triangle B, we do the same thing, only the adjacent side is 3/2.

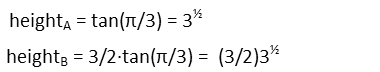
This gives us a rise of:

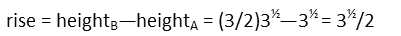
The run is just the difference of the midpoints of the two triangles:

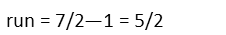
This gives us the following slope for our line:

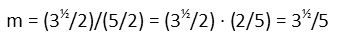
Once we have the slope of the line, we need to find its y-intercept so we can finish its equation. We do this by starting the line equation, with the known slope:

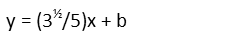
For the y value, we can plug in the height of either Triangle A or Triangle B. I’ll choose A’s height. For the x value, we plug in the midpoint of that same triangle’s base. That’s just 1 for Triangle A, which is why I chose that triangle (makes the math a little easier).

Now I recognize that point a can be defined in terms of x:

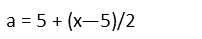
With that, I also note that the height of Triangle C is found in the same manner as the heights of A and B, only the base of the right triangle we use to find it has a length of (x - 5)/2 (the distance from 5 to x, divided by 2). We set the expression for that height equal to the line equation, but we have to be careful to plug the value for our midpoint a in for x in the line equation, or we’re going to actually have called x two different things, and our math will come out all wrong.

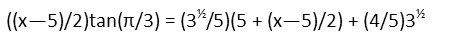
The tangent of π/3 is the square root of three, so let’s show that:

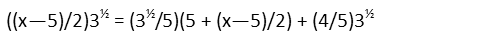
And that’s awfully convenient – we have a square root of three being multiplied by all terms on the left and right-hand sides of the equation, so we can just cancel them all out. *Poof* they go away. We can then get all the x’s on the same side of the equation by subtracting the right-hand x term from both sides.

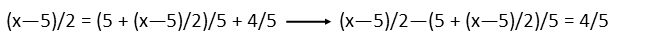
On the left-hand side, we need a common denominator, so we multiply the first fraction by 5/5 and the second by 2/2 to give us one. Once we have that, we can add the two fractions and distribute that 5 and 2 in both terms of the denominator.

We then combine like terms in the denominator. Following that, we can multiply both sides of the equation by 10, and then move the constants to the same side of the equation by adding 30 to both sides. Our final step in solving for x is to divide both sides of the equation by 4.

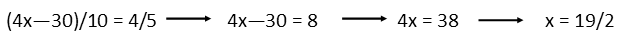
Having found x, we’re not done. Remember, we’re trying to prove a ratio of the triangles. All we’ve done so far is find the x-coordinate of the right-hand side of Triangle C. But using that, we can easily determine the base of C. It is just that coordinate minus 5.

Now that we have the base, we recognize that the ratio of the triangles is just the ratio of the bases, so we place Triangle C’s base of 9/2 over Triangle B’s base of 3, and simplify.

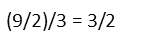
And we see that the ratio of C:B is identical to the 3:2 ratio of B:A.

For an added challenge, find another way to prove this problem that does not involve the line equation.