Math Made Easy: Problem of the Day 96

Exponential equations can always be solved by making use of logarithms. Up until now, in the Problems of the Day, I have avoided doing so because it’s not always necessary. And when you don’t need to, don’t. So the first thing you always want to check when you’re given an exponential equation, is whether there’s some amount of algebra you can do to give them common bases, which will allow you to simply solve the problem be equating the exponents. In cases where you cannot do this, you usually will need to make use of logarithms and their properties.

When we examine today’s problem, we see we have bases of 2 and 10. And, without any hideous juggling of decimal exponents, there’s no pretty way we’re going to give them the same base. To give a base of 2, we’d have to express 10 as 2^1/log2, or 2^{1/0.30102999566}, and that’s just ugly, not to mention we already just made use of the logarithm. So we may as well do it right if we’re going to do it at all.

Seeing that we can’t give them a decent common base, we rewrite the equation placing each term inside a logarithm. This doesn’t change the value of the equation at all since we did it to both sides.

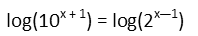
We then take advantage of the properties of logarithms any exponent inside a logarithm is the same thing as that exponent being pulled outside and simply multiplying the logarithm, so let’s do that to both sides and pull those exponents out.

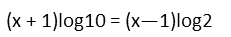
Now that we have that, let’s distribute the logarithms on both sides.

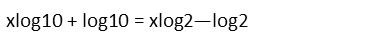
We’re trying to solve for x, so let’s move all the terms with it to one side of the equation and all the terms without it to the other side, adding and subtracting as we need to move them.

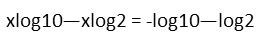
I don’t like that we have so many negative signs, so let’s pretty that up a bit by multiplying everything by -1. Since we’re doing it to both sides, it doesn’t change anything but appearance.

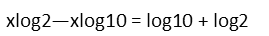
We can factor an x out of both terms on the left-hand side of the equation, so let’s do so. It’s desirable because we’re trying to get it alone, and factoring it out will help us do so.

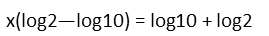
The last step to get x alone will be to divide both sides of the equation by the parenthetical.

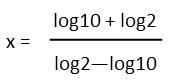
One last thing – we can recognize that log10 is 1. We know this because a logarithm is basically a little question. It is saying: What number do I have to raise my base by to get this number here? And if the base of a logarithm isn’t specified, by convention it is deemed to be a base 10. So log10 is asking what number do I have to raise 10 by to get 10? And that’s 1. So we can replace all the log10 terms with 1. At this point, leaving the fraction is the most accurate form for our answer, but we can also approximate it, getting about -1.857.

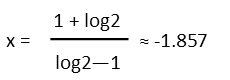
The whole point of the invention of logarithms waaaaay back in the 17th century was an attempt to simplify multiplication and exponentials. This was something of interest back then since they didn’t have calculators to help, so anything to simplify complicated math was much desired. And, despite how scary they can seem, they really do accomplish what Napier and Burgi intended, as I hope you were able to see in following the process for today’s problem. Just like any other mathematical tools, just remember they have a purpose, they’re one more item in your arsenal, and be glad you can make use of them when you want or need, and don’t have to when you’d rather use something else.