Math Made Easy: Problem of the Day 97

Why would someone want to make toast in the middle of a field? Why not? Don’t you want to make toast in the middle of a field now? Anyway, it may not seem like we have a lot of information, but we actually have plenty. So let’s consider what we need to find our answer.

The amount of power the toaster can generate will be determined by the amount of current that reaches it. The current is inversely proportional to the voltage of the circuit. So we can determine the amount of current necessary to run the toaster with the following equation.

Since America uses different voltage than most of the rest of the world, I’ll do two solutions side by side for this problem. On the left, I’ll use America’s 110V circuitry, and on the right, a more global 220V circuitry. So, plugging those into the equation we have for current, we find that, in America, the toaster needs 8 amps of current to run, and in most of the rest of the world, only 4 amps.

Now that we know how much current the toaster needs, we can figure out the maximum allowed resistance of the extension cord. Current is inversely proportional to resistance – as one increases, the other decreases. We can use the following equation to determine the resistance on the circuit that will produce the amperage we need. Any more resistance and the amperage will be too low. We see that the American circuit allows for less resistance than the global circuit.

The resistance of any object is determined by its length, resistivity, and cross-sectional area. Since we’re using a specific gauge, we know the cross-sectional area of our wire (or at least its effective cross-sectional area since it’s stranded). We also know the resistivity of copper. Our equation for the length of the wire we find from the equation for resistance of an object.

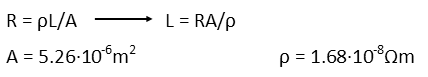
With our known values, and the maximum allowable resistance we calculated, we can now find the maximum length of the wire.

This problem actually demonstrates the advantages of 220V current over 110V. Not only does it require less current to produce the same amount of power (which is not only more efficient, but it means the circuitry is less likely to overheat and cause a fire), but wires can be longer, allowing the same current to effectively travel a longer distance. This problem also demonstrates nicely the use of mathematics in the real world. If you want to run an electric device on a long extension cord, it might be useful to be able to calculate ahead of time the longest cord you can use for given gauges, which can help for planning.