Math Made Easy: Problem of the Day 98

How do astronomers determine the distance of objects in the sky? There are a couple techniques, but the one which has been used for the longest time is parallax. This is the same way your brain is able to determine the distance of anything you see and plot the three-dimensional map that is the image you see of the world around you. Any object, when viewed from two different positions, will appear to be slightly displaced. The first position will see it in one spot relative to its background, the other observer a slightly different one. You can draw a line from each point of observation to the target, and see that they make an angle. The bigger that angle, the closer the object. The smaller the angle, the further the object.

But the distance of the points of observation from each other also affect that angle. The closer they are, the smaller the angle, and the further apart, the bigger the angle. This has the effect of limiting how accurately two points of observation can be used to determine the distance of an object. For our eyes, being close together, they can’t really judge the distance of far-off objects well. They work great for things close, but their base, or distance apart, is just too small.

This effect is called parallax. You’ve probably noticed parallax, and how objects closer to you seem to move more relative to their background when you move about. Look out your car window, the trees closer to you seem to move more than the trees in the background. That’s because you’re changing your observation points, and the angle between those points is changing, but, for the closer trees, it changes more than it does for the farther trees.

In astronomy, we have to deal with the fact that the objects we’re looking at are very, very far away. This means that, even if we move to opposite sides of the Earth, the base of our two observations points isn’t necessarily big enough to determine how far away those objects are – that angle is still just too small. In fact, Aristarchus, the an ancient Greek who presented the first heliocentric model of the solar system way back in the third century B.C., realized that the stars must be incredibly far away, because no matter where he observed them, he couldn’t see any parallax. They just didn’t seem to move. With the instruments of the time back then, no discernible movement relative to their background could be seen in the stars. The angle of parallax is just that small for their distance. It wasn’t until the 18th century that anyone was even able to attempt to measure it – James Bradley tried first on his telescope, but he couldn’t do it. Friedrich Bessell logged the first successful such measurement in 1838.

How do we measure it successfully? Well, now we have much better telescopes, and we have much wider bases available. Typically, we take a photo of the star’s position at a particular time of night, and log the date and time. Then, exactly 6 months later, we take another. Then we compare the two photos and measure any apparent movement. The reason we take the photographs 6 months apparent, is this puts one measurement on one side of the Earth’s orbit, and the other on the opposite side of the Earth’s orbit. So we’re using the diameter of Earth’s orbit around the sun as our baseline, which is quite large indeed. But even with that large a baseline, the angles are tiny.

To give you an idea of how tiny they are, do this right fast. Make a fist. Extend your pinky finger and raise it so you can look at it edgewise. Extend your arm all the way and keep looking at the edge of your pinky finger. The width of your pinky finger as you see it at the end of your arm? That’s about 1 degree of arc as measured in the sky. That degree is broken up into 3600 arc seconds. The parallax we see in any given star is a fraction of that. In fact, the closest star, Proxima Centauri, is 4.24 light years away. That is less than one parsec. And a parsec is defined as the distance an object needs to be for its observed parallax in observations 6 months apart to be only 1 arc second. So that means that, were you to take photos of Proxima Centauri at intervals of 6 minutes, it would only appear to move less than 1/3600th of the width of your pinky. That’s tiny.

So back to our object. It appears to move an entire pinky finger. So how close is it? Well, we remind ourselves that that pinky finger is about 1 degree wide, and that 1 degree is 3600 arc seconds.

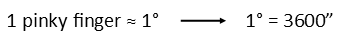
We then remind ourselves of the definition of a parsec in mathematical terms, that it is inversely related to distance:

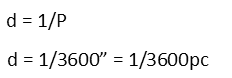
So we calculate that our object is 1/3600th of a parsec away. But how far is that really? Let’s convert the units. A parsec is about 31 trillion kilometers away, or about 3.26 light years. So let’s convert it into kilometers and light years.

That object is REALLY close. In fact, it’s closer than the further manmade object. Voyager 1 holds that distinction, and it’s over 20 billion kilometers away, which is a bit over twice as far as what we just calculated for our object. So, really, I hope it’s not a star, otherwise things are probably pretty toasty right about now. That it appears stationary should be concerning, because it’s proximity means it’s in our solar system, and any object in our solar system should be moving, so we should be asking ourselves why isn’t this thing doing so?

Thankfully, we haven’t seen such an object. This was just a fun exercise.