Math Made Easy: Problem of the Day 33

It’s time for another physical problem. This time we’re going to talk about sound. (Note for sound people out there: I know speakers are more complicated than this – we’re making a simplified case for the sake of introduction to sound). Here’s our problem:

Since the walls are acoustic-dampening, we don’t have to worry about sound reflections, which means no worrying about constructive or destructive interference patterns. There are only two things we have to consider here: the inverse square law for sound (the fact that sound, like any radially propagating phenomenon, drops off, or becomes weaker, with the square of the distance travelled), and how to relate it in a way that we can understand. Since the inverse square law comes into effect, we need to calculate the distance from the speaker on the floor to the ears of the observer. We want to consider an observer at the furthest possible point in the room, so we’ll put our club-goer in the opposite corner. Just like with the light in our previous problem (Problem of the Day 6), we can consider two triangles to describe this, the first being that formed by the walls and the two corners, and the second being the one formed by the hypotenuse of the first triangle, the height of the observer (we’ll just use an even 2 meters for our purposes), and the new diagonal formed. We get a distance about 56.6 meters this way.

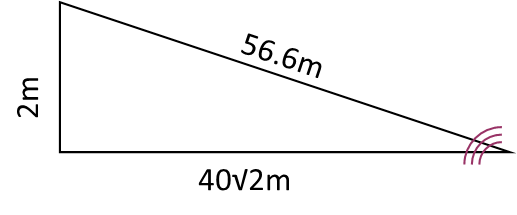
Now we use the inverse square law for sound to calculate its intensity at that distance. Thankfully, we have a form that relates the power output (here the variable P represents the power output of the speaker, and r is the distance from the speaker to the listener). It’s actually quite nice that the distance is squared – it actually undoes the square root we did in the last step of calculating the distance, so I’ll just plug in the 3209 which we know is the exact square of the distance from that last step.

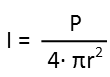
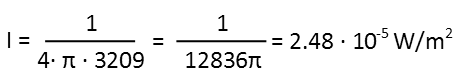
Since watts per square meter is not a unit we’re used to thinking about, and even for scientists is not a very relatable unit, we’ll convert that to decibels. That’s the whole reason the decibel scale exists – the range of what humans can hear, intensity-wise, is so broad, that we needed a logarithmic scale to make it all make more sense to use. For decibels, that just means that something that is 10 decibels louder than something else is 10 times as loud. Something 20 decibels louder is 100 times louder (10 times the sound that is 10 times louder). 30 decibels louder is 1000 times as loud, and so forth. Here’s the equation we use to convert from watts per square meter to decibels:

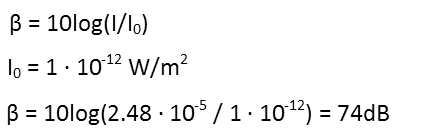
After plugging in our intensity, we find that, to the person in the corner, the loudest sound coming out of that speaker is going to be about 74 decibels. That’s louder than a normal conversation, but not as loud as a telephone dial tone. This means patrons will be able to hear other conversations over the music. It’s a decent sound level, but isn't be loud enough, because you don’t want the sum of the conversations in the room to drown out the music in a dance club, and that’s probably to happen at that sound level (especially since only the LOUDEST sounds produced by the speaker are going to be that loud). But before he decides to get another speaker, let’s consider the sound at 10 meters from the speaker:

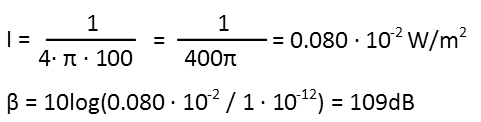
That will be 109 decibels, which is getting close to as loud as a rock concert at 115dB. Since at best the sound will be additive, he’s safe in getting another speaker, and probably should.

Now, I know that if you’re a sound guy, you’re probably pulling your hair out by now – a different formula is used, because the sound a speaker puts out isn’t as straight-forward as I just made it out to be – the power comes from the amp, the speaker is measured in sensitivity, only the loudest sounds the speaker makes would be that loud, etc. I purposefully tried to keep this on an introduction to sound level.