Math Made Easy: Problem of the Day 77

More physics, hooray! This is a thermodynamics problem. As with any problem, first consider the situation, and break it down into parts as you can. Always, always, always diagram when you can. For our diagram of this problem, we recognize that we basically have two cylinders: one of the air inside the can, and one of the aluminum can itself.

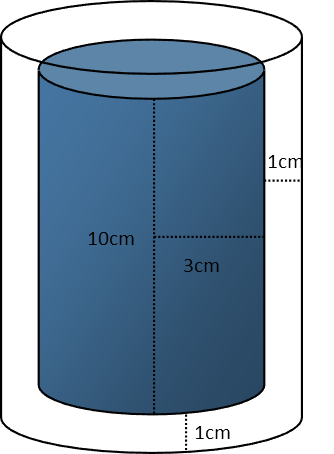
When we draw our diagram, we can see that the height of the air inside the can is 2 centimeters less than the height of the can itself, since the cans walls are all 1cm thick. We subtract one centimeter for the top wall, and one for the bottom wall. For the radius of the cylinder of air, we only subtract one centimeter, since only one of the walls of the can is included in that.

Let’s now calculate the volume of air in the can. Reminding ourselves of the formula for volume of a cylinder, we plug in our radius and height of the cylinder of air. Note that I freely convert from cubic centimeters to milliliters, since they are essentially the same thing.

For the volume of aluminum, we recognize that, since it is essentially a shell, or a solid cylinder with an inner cylinder removed, we calculate its volume by subtracting the volume of air from what the volume of the aluminum would be were it solid. I’ll express that latter volume in terms of the radius and height of the cylinder of air just to keep my r and h consistent.

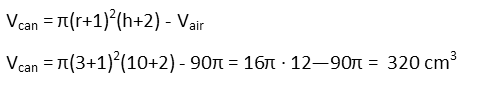
To figure out how much the temperature of the can increases, we must first find the increase of the temperature of the air inside it. That’s caused when the pressure increases, but the volume remains the same. That happens because all those air molecules get excited when you start squeezing them together. They want to expand, but you’re not giving them any room to do so, which makes them start bouncing all around crazy-like. That motion is essentially heat, and Temperature is a measure of an object’s tendency to give it up – the air’s temperature goes up because it wants to get rid of the extra energy. We can find the increase of its temperature using the Ideal Gas Law, and solving for temperature. Note I replace the P with ΔP and T with ΔT since we’re concerned about changes in both, not the actual pressure and temperatures. P represents pressure, V, volume, n the number of moles of a substance (in this version of the Ideal Gas Law), R is basically a conversion constant, and T is temperature.

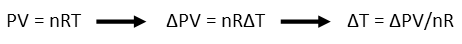
We remind ourselves of the value for R in terms of atmospheres, and calculating the moles of air based on the volume and knowledge of the density of air at room temperature, and its molar mass, then plug everything into our formula and solve.

This seems like a huge increase in temperature, but wait a moment. It just tells us the change in the temperature of the air, NOT of the aluminum. To find that, we need to find out how much energy went into heating up the air. We can use the heat equation from Problem of the Day 38 for that.

Now we calculate the mass of the air in the can, and remind ourselves of its heat capacity at room temperature. We can then calculate the amount of energy added to the air by the increase in temperature – this is the energy the air in the can will impart to the aluminum by thermal contact.

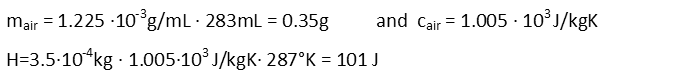
That really wasn’t all that much energy added, was it? So we can feel a little better that the temperature increase seemed so large. We’ll feel even better about it after we calculate the increase of the aluminum’s temperature as the system comes to equilibrium. Calculating the mass of the aluminum, and reminding ourselves of the specific heat capacity of aluminum, we then rearrange the heat equation to solve for temperature change of the aluminum. Then we plug all our numbers in and solve.

Look at that, it barely budged. That’s due to two things: Aluminum has a much lower heat capacity than air, and there are a lot more aluminum atoms for the air molecules to crash into – therefor more atoms to distribute the incoming heat, which means a lower increase in temperature. And that’s a GOOD thing. Carbonation in a soda can is capable of increasing the pressure of the can to 2 atmospheres, easily. Even though the walls of the can are much thinner than the one in our problem today, we have the advantage of the soda being denser than air, so its temperature doesn’t experience that big an increase, and the aluminum is denser than the liquid, so it acts as a nice insulator. That’s added to the fact that the walls of the can bulge in reality, so the volume increases a little bit, as well, which also helps keep the temperature from increasing.